题目内容
将抛物线y=-x2向右平移2个单位后的抛物线的解析式是( )
| A、y=-(x-2)2 |
| B、y=-(x+2)2 |
| C、y=-x2-2 |
| D、y=-x2+2 |
考点:二次函数图象与几何变换
专题:
分析:求出向右平移后的顶点坐标,然后写出即可.
解答:解:抛物线y=-x2的顶点坐标为(0,0),
右平移2个单位后抛物线的顶点坐标为(2,0),
所以,平移后的抛物线解析式为y=-(x-2)2.
故选A.
右平移2个单位后抛物线的顶点坐标为(2,0),
所以,平移后的抛物线解析式为y=-(x-2)2.
故选A.
点评:本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并用根据规律利用点的变化确定函数解析式.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
下列抛物线,对称轴是x=-
的是( )
| 1 |
| 2 |
A、y=-
| ||
B、y=x2-
| ||
C、y=x2+x-
| ||
D、y=x2-x-
|
下列调查中,适宜采用全面调查(普查)方式的是( )
| A、调查全国青少年儿童的睡眠时间 |
| B、调查本班50名同学的身高情况 |
| C、调查我市居民的年人均消费 |
| D、调查某日光灯管厂一批灯管的使用寿命 |
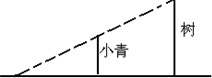 一天,小青在校园内发现:旁边一颗树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为1.60米,由此可推断出树高是
一天,小青在校园内发现:旁边一颗树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为1.60米,由此可推断出树高是 如图,在梯形ABCD中,AD∥BC,∠A=∠B=90°,BC=4AD.AB为⊙O的直径,OA=2,CD与⊙O相切于点E,求CD的长.
如图,在梯形ABCD中,AD∥BC,∠A=∠B=90°,BC=4AD.AB为⊙O的直径,OA=2,CD与⊙O相切于点E,求CD的长. 如图,在⊙O中,直径AB⊥弦CD,垂足为P,OB=5,PB=2,求CD的长.
如图,在⊙O中,直径AB⊥弦CD,垂足为P,OB=5,PB=2,求CD的长.