题目内容
在圆内接四边形ABCD中，对角∠A与∠C的度数之比是4：5，求∠C的度数．
考点：圆内接四边形的性质
专题：
分析：利用对角∠A与∠C的度数之比是4：5，可设∠A=5x，则∠C=4x，根据圆内接四边形的性质得5x+4x=180°，解得x=20°，然后计算4x即可．
解答：解：设∠A=5x，则∠C=4x，
∵四边形ABCD为圆内接四边形，
∴∠A+∠C=180°，
即5x+4x=180°，
解得x=20°，
∴∠C=4x=80°．
∵四边形ABCD为圆内接四边形，
∴∠A+∠C=180°，
即5x+4x=180°，
解得x=20°，
∴∠C=4x=80°．
点评：本题考查了圆内接四边形的性质：圆内接四边形的对角互补．
练习册系列答案
相关题目
小林放学后，先向东走了300米，再向北走了200米，到书店A买了一本书，后向西走了500米，再向南走了100米，到了快餐店B买了零食，又向南走了400米，再向东走了800米，到了家C，如图请在坐标系中画出A，B，C的位置，并用坐标表示出来．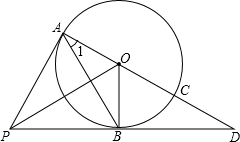
如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，AC、PB的延长线相较于点D．
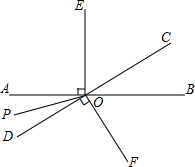如图，直线AB与CD相交于点O，OP是∠AOD的平分线，OE⊥AB，OF⊥CD．
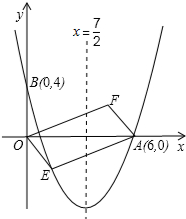如图，对称轴为直线x=