题目内容
16.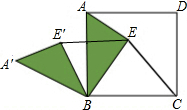 小明在探究问题“正方形ABCD内一点E到A、B、C三点的距离之和的最小值”时,由于EA、EB、EC比较分散,不便解决.于是将△ABE绕点B逆时针旋转60°得△A′BE′,连接EE′.
小明在探究问题“正方形ABCD内一点E到A、B、C三点的距离之和的最小值”时,由于EA、EB、EC比较分散,不便解决.于是将△ABE绕点B逆时针旋转60°得△A′BE′,连接EE′.(1)△EBE′是等边三角形;
(2)若正方形ABCD的边长为2,则AE+BE+CE的最小值是$\sqrt{6}$+$\sqrt{2}$.
分析 (1)根据旋转的性质得BE=BE′,∠EBE′=60°,则利用等边三角形的判定可判断△EBE′为等边三角形;
(2)连结A′C,如图,由△EBE′为等边三角形得到EE′=BE,再利用旋转的性质得A′E′=AE,BA′=BA=2,∠ABA′=60°,根据两点之间线段最短得A′E′+E′E+EC≥A′C,所以AE+BE+CE≥AC(当且仅当点E′、点E在AC上时,取等号),则AE+BE+CE有最小值,最小值为A′C的长,作A′H⊥BC于H,如图,先在Rt△A′BH中,利用含30度的直角三角形三边的关系得到A′H=$\frac{1}{2}$A′B=1,BH=$\sqrt{3}$A′H=$\sqrt{3}$,然后在Rt△A′CH中,利用勾股定理可计算出A′C=$\sqrt{6}$+$\sqrt{2}$,于是得到AE+BE+CE的最小值是$\sqrt{6}$+$\sqrt{2}$.
解答 解:(1)∵△ABE绕点B逆时针旋转60°得△A′BE′,
∴BE=BE′,∠EBE′=60°,
∴△EBE′为等边三角形;
(2)连结A′C,如图,
∵△EBE′为等边三角形,
∴EE′=BE,
∵△ABE绕点B逆时针旋转60°得△A′BE′,
∴A′E′=AE,BA′=BA=2,∠ABA′=60°,
∵A′E′+E′E+EC≥A′C,
∴AE+BE+CE≥AC(当且仅当点E′、点E在AC上时,取等号),
∴AE+BE+CE有最小值,最小值为A′C的长,
作A′H⊥BC于H,如图,
在Rt△A′BH中,∠A′BH=30°,
∴A′H=$\frac{1}{2}$A′B=1,BH=$\sqrt{3}$A′H=$\sqrt{3}$,
∴CH=2+$\sqrt{3}$,
在Rt△A′CH中,A′C=$\sqrt{A′{H}^{2}+C{H}^{2}}$=$\sqrt{{1}^{2}+(2+\sqrt{3})^{2}}$=$\sqrt{8+4\sqrt{3}}$=$\sqrt{(\sqrt{6}+\sqrt{2})^{2}}$=$\sqrt{6}$+$\sqrt{2}$.
∴AE+BE+CE的最小值是$\sqrt{6}$+$\sqrt{2}$.
故答案为:等边,$\sqrt{6}$+$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质和勾股定理.

| A. | $2{x^2}+\frac{1}{x}-1=0$ | B. | ax2+bx+c=0 | C. | 2x2+1=0 | D. | x2+2xy+y2=0 |
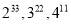 ; ____________________
; ____________________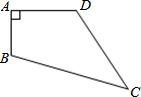 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积36cm2.
已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积36cm2.