题目内容
6.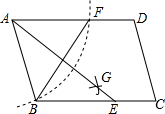 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解答 解:连结EF,AE与BF交于点O,如图,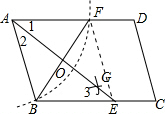
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AE=2AO=8.
故选C.
点评 本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.

练习册系列答案
相关题目
16.一个物体从A点出发,沿坡度为1:7的斜坡向上直线运动到B,AB=30米时,物体升高( )米.
| A. | $\frac{30}{7}$ | B. | 3$\sqrt{2}$ | ||
| C. | $\frac{30}{6}$ | D. | 以上的答案都不对 |
18.下列四个几何体中,主视图为圆的是( )
| A. |  | B. |  | C. |  | D. |  |





 过点(0,-2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m).
过点(0,-2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m). 如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,