题目内容
7. 在平行四边形ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
在平行四边形ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;
(2)若CF=9,BF=12,DF=15,求证:AF平分∠DAB.
分析 (1)根据平行四边形的性质得出DC∥AB,即DF∥BE,根据平行四边形的判定得出四边形DEBF为平行四边形,根据矩形的判定得出即可;
(2)根据矩形的性质求出∠BFC=90°,根据勾股定理求出BC,求出AD=DF,推出∠DAF=∠DFA,求出∠DAF=∠BAF,即可得出答案.
解答 证明:(1)∵四边形ABCD为平行四边形,
∴DC∥AB,即DF∥BE,
又∵DF=BE,
∴四边形DEBF为平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴四边形DEBF为矩形;
(2)∵四边形DEBF为矩形,
∴∠BFC=90°,
∵CF=9,BF=12,
∴BC=$\sqrt{{9}^{2}+1{2}^{2}}$=15,
∴AD=BC=15,
∴AD=DF=15,
∴∠DAF=∠DFA,
∵AB∥CD,
∴∠FAB=∠DFA,
∴∠FAB=∠DFA,
∴AF平分∠DAB.
点评 本题考查了平行四边形的性质和判定,矩形的性质和判定,勾股定理,平行线的性质,角平分线定义的应用,能综合运用性质进行推理是解此题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
17.已知实数x=4,y=8,则以x,y的值为两边长的等腰三角形的周长是( )
| A. | 20 | B. | 16 | C. | 20或16 | D. | 以上答案均不对 |
2.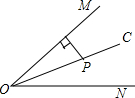 如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )
如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )
 如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )
如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )| A. | 2cm | B. | 3cm | C. | 5cm | D. | 6cm |
12.下列方程中,关于x的一元二次方程是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | x2+2x-1=0 | D. | x2+2x=x2-1 |
19. 如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )
如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )
 如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )
如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.在数轴上满足-$\sqrt{3}$和$\sqrt{5}$的两点之间的距离公式是( )
| A. | $\sqrt{3}$-$\sqrt{5}$ | B. | $\sqrt{3}$+$\sqrt{5}$ | C. | $\sqrt{5}$-$\sqrt{3}$ | D. | -($\sqrt{3}$+$\sqrt{5}$) |
