题目内容
关于x的一元二次方程(a-1)x2+2x-1=0有实数根,则a的范围为 .
考点:根的判别式,一元二次方程的定义
专题:
分析:由一元二次方程(a-1)x2+2x-1=0有实数根,则a-1≠0,即a≠1,且△≥0,即△=22-4(a-1)×(-1)=4a≥0,然后解两个不等式得到a的取值范围.
解答:解:∵一元二次方程(a-1)x2+2x-1=0有实数根,
∴a-1≠0即a≠1,且△≥0,即有△=(-2)2-4(a-1)×(-1)=4a≥0,解得a≥0,
∴a的取值范围是a≥2且a≠1.
故答案为:a≥0且a≠1.
∴a-1≠0即a≠1,且△≥0,即有△=(-2)2-4(a-1)×(-1)=4a≥0,解得a≥0,
∴a的取值范围是a≥2且a≠1.
故答案为:a≥0且a≠1.
点评:此题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次方程的定义.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
函数y=-6x2的最值是( )
| A、最大值6 | B、最小值-6 |
| C、最小值0 | D、最大值0 |
在△ABC中,AD为∠BAC的平分线,DE⊥AB,F为AC上一点,且∠DFA=120°,则DE与DF的关系为(自己画图)( )
| A、DE>DF |
| B、DE<DF |
| C、DE=DF |
| D、不能确定DE与DF的大小 |
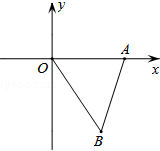 如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,-3),△EFD是△ABO关于原点O的位似图形,且原图形与它位似比为2,则点F的坐标为
如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,-3),△EFD是△ABO关于原点O的位似图形,且原图形与它位似比为2,则点F的坐标为 如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,HN=c,则a、b、c三者间的大小关系为
如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,HN=c,则a、b、c三者间的大小关系为 如图所示,在半圆O中,半径OC与直径AB垂直,E、F分别是CO、AO上的点,且OE=OF,求证:BD⊥CF.
如图所示,在半圆O中,半径OC与直径AB垂直,E、F分别是CO、AO上的点,且OE=OF,求证:BD⊥CF.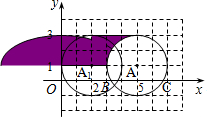 如图,在平面直角坐标系中,以A(5,1)为圆心,2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
如图,在平面直角坐标系中,以A(5,1)为圆心,2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题: