题目内容
3.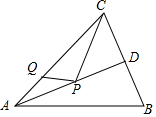 如图,在△ABC中,AB=AC=13,BC=10,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{120}{13}$.
如图,在△ABC中,AB=AC=13,BC=10,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{120}{13}$.
分析 先判断出PC+PQ的最小值时,点M的位置,得出最小值就出CM,利用勾股定理求出AD,最后用等面积法求出CM即可.
解答 解:如图,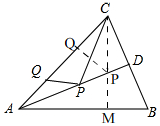 作出点Q关于AD的对称点M,
作出点Q关于AD的对称点M,
∵AD是∠BAC的平分线,
∴点M在边AB上,
连接CM交AD与P,当CM⊥AB时,PC+PQ的最小值是CM.
∵AB=AC=13,BC=10,AD是∠BAC的平分线,
∴AD⊥BC,BD=$\frac{1}{2}$BC=5,
根据勾股定理得,AD=12,
利用等面积法得:AB•CM=BC•AD,
∴CM=$\frac{BC•AD}{AB}=\frac{10×12}{13}$=$\frac{120}{13}$
故答案为:$\frac{120}{13}$.
点评 此题是轴对称-最短路线问题,主要考查了角平分线的性质,对称的性质,勾股定理,等面积法,用等面积法求出CM是解本题的关键.

练习册系列答案
相关题目
13.能使分式方程$\frac{k}{1-x}$+2=$\frac{3}{x-1}$有非负实数解且使一次函数y=(k+2)x-1的图象不经过第一象限的所有整数k的积为( )
| A. | 20 | B. | -20 | C. | 60 | D. | -60 |
14. 如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )
如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )
 如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )
如图,如果把张军前面的第2个同学李智记作+2,那么-1表示张军周围的同学是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
11.一元二次方程3x2-5x+1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
8.用四舍五入法对2.098176分别取近似值,其中正确的是( )
| A. | 2.09(精确到0.01) | B. | 2.098(精确到千分位) | ||
| C. | 2.0(精确到十分位) | D. | 2.0981(精确到0.0001) |
13.如果整式xn-3-5x+2是关于x的四次三项式,那么n等于( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |