题目内容
8.阅读材料:如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有:那么有x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.这是一元二次方程根与系数的关系,我们利用它来解题.例:已知x1,x2是方程x2+6x-3=0的两根,求x12+x22的值
解法可以是这样:∵x1+x2=-6,x1x2=-3,则x12+x22=(x1+x2)-2x1x2=(-6)2-2×(-3)=42
请你根据以上解法解答下题:已知x1,x2是方程x2-4x+2=0的两根,求:
(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值;(2)x12+x22的值.
分析 (1)根据一元二次方程根与系数的关系,可以求得两根之积或两根之和,欲求$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值,根据$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$代入数值计算即可;
(2)根据一元二次方程根与系数的关系,可以求得两根之积或两根之和,欲求x12+x22的值,根据x12+x22=(x1+x2)2-2x1x2,代入数值计算即可.
解答 解:∵x1,x2是方程x2-4x+2=0的两根,
∴x1+x2=4,x1x2=2,
(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{4}{2}$=2;
(2)x12+x22=(x1+x2)2-2x1x2=16-4=12.
点评 此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
19. 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 1.4 |
3.若$\sqrt{x-1}$+(y+3)2=0,则x-y的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -7 |
13.某公司的仓库中原先有1.5万件货物,后又运出0.7万件,过了一段时间后计划往仓库中补充1.2万件,但因为某些原因,少往仓库中补充0.3万件,则现在仓库中的货物有( )
| A. | 1.8万件 | B. | 1.7万件 | C. | 1.5万件 | D. | 1.1万件 |
17.已知关于x的一元二次方程x2-x-1=0的两根分别为x1、x2,则|x1-x2|的值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 1+$\sqrt{5}$ |
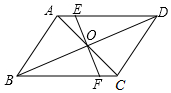 如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.