题目内容
已知二次函数y=﹣x2+2x+1的顶点为A,与y轴交点为B,动点P(x,0)在x轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. (﹣1,0) B. (1,0) C. (﹣ ,0) D. (
,0) D. ( ,0)
,0)
A 解:∵y=﹣x2+2x+1=﹣(x2﹣2x)+1=﹣(x﹣1)2+2,
∴A(1,2).
∵当x=0时,y=1,
∴B(0,1).
令直线AB的解析式为y=kx+b(k≠0),
∴ ,解得
,解得 ,
,
∴直线AB的解析式为y=x+1.
∵|AP﹣BP|≤AB,
∴当点P在直线AB上时,线段AP与线段BP之差最大,
∵P(x,0),
∴x+1=0,解得x=﹣1,
∴P(﹣1,0).

练习册系列答案
相关题目

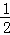 ,求⊙O的直径.
,求⊙O的直径.