题目内容
解方程：x2+6x-5=0．
考点：解一元二次方程-配方法
专题：
分析：利用配方法解方程．配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．
解答：解：∵x2+6x-5=0，
∴x2+6x=5，
∴x2-6x+32=5+32，
即（x-3）2=14，
∴x=3±
，
∴原方程的解是：x1=3-
，x2=3+
．
∴x2+6x=5，
∴x2-6x+32=5+32，
即（x-3）2=14，
∴x=3±
| 14 |
∴原方程的解是：x1=3-
| 14 |
| 14 |
点评：此题考查了配方法解一元二次方程，解题时要注意解题步骤的准确应用．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
练习册系列答案
阅读快车系列答案
相关题目
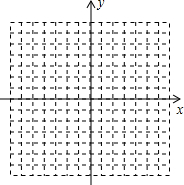如图，方格纸中每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点在格点上．且A（1，-4），B（5，-4），C（4，-1）