题目内容
17.已知关于x,y的方程组$\left\{\begin{array}{l}{x+2y=5k-2}\\{x-y=-k+4}\end{array}\right.$的解是一对异号的数(1)求k的取值范围;
(2)化简|k+2|+|k-1|.
分析 (1)把k看做已知数表示出方程组的解,根据x与y异号求出k的范围即可;
(2)由k的范围判断绝对值里边式子的正负,利用绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=5k-2①}\\{x-y=-k+4②}\end{array}\right.$,
①-②得:3y=6k-6,即y=2k-2,
①+②×2得:3x=3k+6,即x=k+2,
根据题意得:xy=(2k-2)(k+2)<0,
解得:-2<k<1;
(2)∵-2<k<1,
∴k+2>0,k-1<0,
则原式=k+2-k+1=3.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在直角△ABC中,AC=5,BC=12,则AB边的长是( )
| A. | 13 | B. | $\sqrt{119}$ | C. | 13或$\sqrt{119}$ | D. | 无法确定 |
9.已知点P(-3,4),则点P到x轴的距离和到y轴的距离分别为( )
| A. | 3,4 | B. | -3,4 | C. | 4,3 | D. | 4,-3 |
7. 如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )
如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )
 如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )
如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )| A. | 120° | B. | 128° | C. | 80° | D. | 100° |
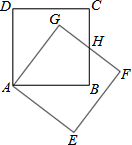 如图,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HC=HF.
如图,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HC=HF.