题目内容
19.已知方程组$\left\{\begin{array}{l}{ax-by=4}\\{2x+3y=4}\end{array}\right.$与$\left\{\begin{array}{l}{ax+by=2}\\{4x-3y=2}\end{array}\right.$的解相同,试求a+b的值.分析 根据题意先解方程组$\left\{\begin{array}{l}{2x+3y=4}\\{4x-3y=2}\end{array}\right.$,再求a,b的值即可.
解答 解:依题意可有$\left\{\begin{array}{l}{2x+3y=4}\\{4x-3y=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=\frac{2}{3}}\end{array}\right.$,
所以,有$\left\{\begin{array}{l}{a-\frac{2}{3}b=4}\\{a+\frac{2}{3}b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=3}\\{b=-\frac{3}{2}}\end{array}\right.$,
因此a+b=3-$\frac{3}{2}$=$\frac{3}{2}$.
点评 本题考查了二元一次方程组的解,掌握二元一次方程组的解法是解题的关键.

练习册系列答案
相关题目
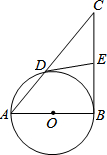 已知:如图,以Rt△ABC的边AB为直径的⊙O交斜边AC于点D,E是BC边的中点,连接DE.
已知:如图,以Rt△ABC的边AB为直径的⊙O交斜边AC于点D,E是BC边的中点,连接DE. 如图,请你用几个基本图形设计三个有具体形象的轴对称图形.
如图,请你用几个基本图形设计三个有具体形象的轴对称图形. 如图,AD∥BC,BD平分∠ABC,∠A=120°,∠C=60°,AB=CD=4cm,求:
如图,AD∥BC,BD平分∠ABC,∠A=120°,∠C=60°,AB=CD=4cm,求: