Question

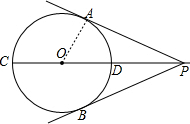
如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P作⊙O的切线PA、PB，切点分别为点A、B．
①当DP=

 

cm时，四边形AOBD是菱形；
②当DP=

 

cm时，四边形AOBP是正方形．

Answer 1

考点：切线的性质,菱形的判定,正方形的判定

专题：

分析：①当四边形AOBD为菱形时，可知AD=AO，且∠AOP=60°，可求得PO=2AO，则可求得PD，可得出结论；
②当四边形AOBP为正方形时，则有PA=OA，再结合切割线定理可求得PD，可得出答案．

解答： 解：①如果四边形AOBD为菱形，则有AD=AO=OD=

1

2

CD=1cm，
∴∠AOP=60°，
如图，连接OA，则OA⊥PA，

∴∠APO=30°，
∴OP=2AO=2cm，
∴PD=OP-OD=1cm，
∴当DP=1cm时，四边形AOBD为菱形；
②当四边形AOBP为正方形时，则有PA=AO=1cm，
∵PA为⊙O的切线，
∴PA²=PD•PC，且CD=2cm，
∴1=PD（PD+2），整理可得PD²+2PD-1=0，
解得PD=

2

-1或PD=-

2

-1（舍去），
∴PD=

2

-1（cm），
∴当PD=（

2

-1）cm时，四边形AOBP为正方形；
故答案为：①1；②（

2

-1）．

点评：本题主要考查切线的性质及正方形、菱形的性质，掌握菱形、正方形的四边相等是解题的关键，解这类问题时，可以把结论当成条件求寻求这个结论成立的条件．