Question

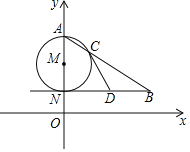
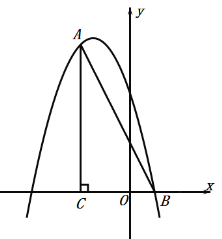
【题目】已知：如图，在△ABC中，，以为直径的⊙O与交于点，，垂足为，的延长线与的延长线交于点．

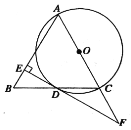
（1）求证：是⊙O的切线.

（2）若⊙O的半径为4，，求的长．

Answer 1

【答案】（1）证明见解析；（2）DE=.

【解析】

（1）如图，连接OD，由DE⊥AB可得∠AED=90°，根据等腰三角形的性质可得∠B=∠ACB，∠ODC=∠ACB，根据等量代换可得∠B=∠ODC，可证明OD//AB，可得∠AEF=∠ODF=90°，即可证明DE是⊙O的切线；（2）根据含30°角的直角三角形的性质可求出OF的长，即可求出AF的长，根据含30°角的直角三角形的性质可求出AE的长，利用勾股定理可求出DF、EF的长，进而可求出DE的长.

如图，连接OD

∵DE⊥AB，

∴∠AEF=90°，

∵AB=AC，

∴∠B=∠ACB，

∵OD=OC，

∴∠ODC=∠ACB，

∴∠B=∠ODC，

∴OD//AB，

∴∠ODF=∠AEF=90°，

∵OD是⊙O的半径，

∴DE是⊙O的切线.

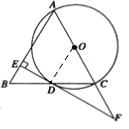
（2）∵∠F=30°，OD=4，OD⊥EF，

∴OF=2OD=8，

∴AF=OF+OA=8+4=12，DF==，

∴AE=AF=6，EF==，

∴DE=EF-DF=-=.