题目内容
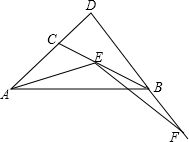如图，△ABD中，C是AD上的一点，且AD=k•DB，DB=k•DC，AC=m•BC，E是直线BC上一点，∠AEF=∠ACB，EF交直线DB于F，试探究AE与EF之间的数量关系．考点：相似三角形的判定与性质
专题：
分析：可先证明△DCB∽△DBA，则可进一步证明△HAE∽△BFE，可得到
=
=
=m，即有AE=mEF．
| AE |
| EF |
| AH |
| BE |
| AE |
| EF |
解答：
解：过点E作EH∥AB交AC于点H，
∵AD=kDB，DB=kDC，∠D=∠D，
∴△DCB∽△DBA，
∴∠AEF=ACB，∠BEF+∠AEF=∠ACB+∠DAE，
∴∠BEF=∠DAE，
∵∠DBC=∠BEF+∠F=∠DAB=∠DAE+∠EAB，
∴∠BFE=∠EAB，
∵EF∥AB，AC=mBC，
∴∠HEA=∠EAB，
∴∠BFE=∠HEA，
=
═m，
∴△HAE∽△BFE，
∴
=
，
∴
=m，
∴AE=mEF．
解：过点E作EH∥AB交AC于点H，∵AD=kDB，DB=kDC，∠D=∠D，
∴△DCB∽△DBA，
∴∠AEF=ACB，∠BEF+∠AEF=∠ACB+∠DAE，
∴∠BEF=∠DAE，
∵∠DBC=∠BEF+∠F=∠DAB=∠DAE+∠EAB，
∴∠BFE=∠EAB，
∵EF∥AB，AC=mBC，
∴∠HEA=∠EAB，
∴∠BFE=∠HEA，
| AH |
| BE |
| AC |
| BC |
∴△HAE∽△BFE，
∴
| AE |
| EF |
| AH |
| BE |
∴
| AE |
| EF |
∴AE=mEF．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的判定方法及相似三角形的对应边成比例是解题的关键．
练习册系列答案
相关题目
如图，在菱形ABCD中，BE⊥AD，垂足为E，且E为AD为中点．则∠ADC=