Question

18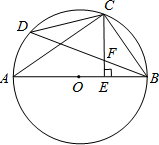．如图，AB是⊙O的直径，C是$\widehat{BD}$的中点，CE⊥AB于点E，BD交CE于点F．
（1）求证：CF=BF；
（2）若CD=6，AC=8，求⊙O的半径及CE的长．

Answer 1

分析 （1）要证明CF﹦BF，可以证明∠1=∠2；AB是⊙O的直径，则∠ACB﹦90°，又知CE⊥AB，则∠CEB﹦90°，则∠2﹦90°-∠ACE﹦∠A，∠1﹦∠A，则∠1=∠2；
（2）在直角三角形ACB中，AB²=AC²+BC²，又知，BC=CD，所以可以求得AB的长，即可求得圆的半径；再根据三角形相似可以求得CE的长．

解答 （1）证明：∵AB是⊙O的直径，
∴∠ACB=90°，∴∠A=90°-∠ABC．
∵CE⊥AB，∴∠CEB=90°，
∴∠ECB=90°-∠ABC，∴∠ECB=∠A．（2分）
又∵C是$\widehat{BD}$的中点，
∴$\widehat{CD}$=$\widehat{CB}$，
∴∠DBC=∠A，
∴∠ECB=∠DBC，
∴CF=BF；

（2）解：∵$\widehat{BC}$=$\widehat{CD}$，
∴BC=CD=6，
∵∠ACB=90°，
∴AB=$\sqrt{BC2+AC2}$=$\sqrt{62+82}$=10，
∴⊙O的半径为5，
∵S_△ABC=$\frac{1}{2}$AB•CE=$\frac{1}{2}$BC•AC，
∴CE=$\frac{BC•AC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$．

点评 此题考查了相似三角形的判定与性质、全等三角形的判定与性质、圆周角定理、等腰三角形的性质以及角平分线的性质等知识．此题综合性很强，难度适中，注意数形结合思想与方程思想的应用，注意辅助线的作法．