题目内容
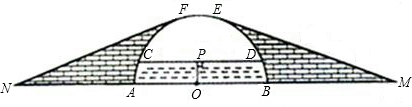
 如图,设半圆的圆心O在直角△ABC的斜边AB上,且与两直角边相切于D、E,若△ABC的面积为S,斜边长为c,则圆的半径为________.
如图,设半圆的圆心O在直角△ABC的斜边AB上,且与两直角边相切于D、E,若△ABC的面积为S,斜边长为c,则圆的半径为________.

分析:连OD,OE,OC,根据切线性质得OD⊥AC,OE⊥BC,设AC=b,BC=a,OD=OE=R,则S△ABC=S△AOC+S△BOC,即
 bR+
bR+ aR=S,
aR=S,得到a+b=
 ,再利用勾股定理得到a+b=
,再利用勾股定理得到a+b= ,这样就可求得R的值.
,这样就可求得R的值.解答:
 解:连OD,OE,OC,如图,
解:连OD,OE,OC,如图,∵D,E为切点,
∴OD⊥AC,OE⊥BC,
设AC=b,BC=a,OD=OE=R,
∵S△ABC=S△AOC+S△BOC,
∴
 bR+
bR+ aR=S,
aR=S,∴a+b=
 ,
,又∵a2+b2=c2,
∴(a+b)2=c2+2ab,
∴a+b=
 ,
,∴
 =
= ,
,∴R=
 .
.故答案为:
 .
.点评:本题考查了切线的性质:圆心与切点的连线垂直切线,过圆心垂直于切线的直线必过切点;过圆外一点引圆的两条切线,切线长相等,也考查了三角形的面积公式和勾股定理以及代数式的变形能力.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为( )
如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为( )| A、15:4 | B、11:3 | C、4:1 | D、3:1 |
 如图,设半圆的圆心O在直角△ABC的斜边AB上,且与两直角边相切于D、E,若△ABC的面积为S,斜边长为c,则圆的半径为
如图,设半圆的圆心O在直角△ABC的斜边AB上,且与两直角边相切于D、E,若△ABC的面积为S,斜边长为c,则圆的半径为