题目内容
15.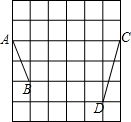 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.(1)在方格纸中画以AB为一边的菱形ABEF,点E、F在小正方形的顶点上,且菱形ABEF的面积为3;
(2)在方格纸中画以CD为一边的等腰△CDG,点G在小正方形的顶点上,连接EG,使∠BEG=90°,并直接写出线段EG的长.
分析 (1)根据题意、菱形的四边相等,菱形面积公式画图即可;
(2)根据等腰直角的性质和题意画图即可.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
EG=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
点评 本题考查的是设计作图、菱形的性质,勾股定理的应用,正确理解题意和菱形的性质是解题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
6.为了解某班学生每天使用零花钱的情况,小明随机查了15名同学,结果如下表:
关于这15名同学每天使用的零花钱,下列说法正确的是( )
| 每天使用零花钱(单位:元) | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A. | 众数是5元 | B. | 极差是4元 | C. | 中位数3元 | D. | 平均数是2.5元 |
7.甲、乙二人在相同条件下各射靶10次,每次射靶成绩如图所示,经计算得:$\overline{{x}_{甲}}$-$\overline{{x}_{乙}}$=1,S${\;}_{甲}^{2}$=1.2,S${\;}_{乙}^{2}$=5.8,则下列结论中不正确的是( )
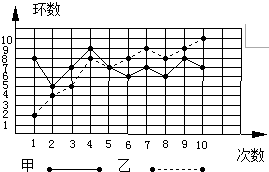

| A. | 甲、乙的总环数相等 | B. | 甲的成绩稳定 | ||
| C. | 甲、乙的众数相同 | D. | 乙的发展潜力更大 |
5.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2+a3=a5 | C. | (a2)3=a6 | D. | (-2x)3=-6x3 |
 如图所示的几何体是由五个大小相同的正方体搭建而成的,它的左视图是( )
如图所示的几何体是由五个大小相同的正方体搭建而成的,它的左视图是( )



 在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上.DF=BE.求证:四边形BEDF是矩形.
在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上.DF=BE.求证:四边形BEDF是矩形.