题目内容
如图，四边形ABCD中，已知AB=10，CD=12，对角线BD平分∠ABC，∠ADB=45°，∠BCD=90°，则边BD的长度为考点：相似三角形的判定与性质,勾股定理
专题：
分析：如图，作辅助线；首先证明△FBD∽△GDA，进而得到DG•DF=BF•AG①；设BE=λ，将①式中的线段分别用λ来表示，得到关于λ的方程，解方程即可解决问题．
解答：
解：如图，过点D作DE⊥AB于点E；在ED上截取EF=EB，EG=EA；
连接AG，BF；则∠BFE=∠AGE=45°，
∴∠BFD=∠DGA=135°；
∵BD平分∠ABC，且∠BCD=90°，
∴DE=DC=12，BE=BC；
∵∠FBD+∠BDF=∠BDF+∠ADG=45°，
∴∠FBD=∠GDA；
∴△FBD∽△GDA，
∴
=
，即DG•DF=BF•AG；
设BE=λ，则DF=12-λ，EG=EA=10-λ；
BF=
λ，AG=
EG=
（10-λ），
∴（λ+2）（12-λ）=
（10-λ）
λ，
整理得：λ2-10λ+24=0，
解得：λ=4或6，
即边BC的长度为4或6．
由勾股定理得：BD2=BC2+CD2，
∴BD=4
或6
故答案为：4
或6
．
解：如图，过点D作DE⊥AB于点E；在ED上截取EF=EB，EG=EA；连接AG，BF；则∠BFE=∠AGE=45°，
∴∠BFD=∠DGA=135°；
∵BD平分∠ABC，且∠BCD=90°，
∴DE=DC=12，BE=BC；
∵∠FBD+∠BDF=∠BDF+∠ADG=45°，
∴∠FBD=∠GDA；
∴△FBD∽△GDA，
∴
| BF |
| DG |
| DF |
| AG |
设BE=λ，则DF=12-λ，EG=EA=10-λ；
BF=
| 2 |
| 2 |
| 2 |
∴（λ+2）（12-λ）=
| 2 |
| 2 |
整理得：λ2-10λ+24=0，
解得：λ=4或6，
即边BC的长度为4或6．
由勾股定理得：BD2=BC2+CD2，
∴BD=4
| 10 |
| 5 |
故答案为：4
| 10 |
| 5 |
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是作辅助线，构造相似三角形；灵活运用有关定理来分析、判断、解答是关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
多项式
中，二次项的系数是（ ）
| -3x2+y |
| 4 |
| A、-3 | ||
| B、1 | ||
C、-
| ||
D、
|
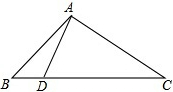已知：△ABC中，AD⊥AC，∠BAD=∠C，AB=4，CD=6．
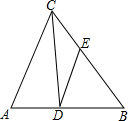如图，在△ABC中，∠ACB的平分线交AB于点D，DE∥AC交BC于点E，若AC=9，CE=3，求BE的长．
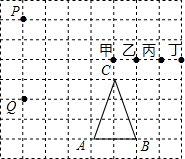如图所示，若ABCPQ甲乙丙丁都是方格纸中的格点．如图，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，为使△PQR∽△ABC，则点R应是甲、乙、丙、丁四点中的（ ）