题目内容
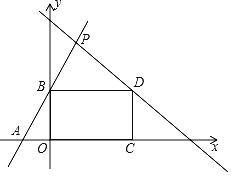
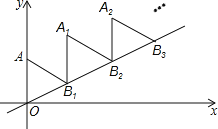
【题目】如图，放置的△OAB1，△B1A1B2，△B2A2B3，都是边长为2的等边三角形，边AO在Y轴上，点B1、B2、B3都在直线y=
x上，则点A2019的坐标为__________________
【答案】
【解析】
根据题意得出，直线AA的解析式为y＝
x＋2，进而得出A，A，A，A坐标，进而得出坐标变化规律，进而求出答案．
如图，过B向x轴作垂线BC，垂足为C
由题意得：A（0，2），AO∥AB，∠BOC＝30°
∴CO＝
∴B的横坐标为，则A的横坐标为
连接AA，可知所有三角形顶点都在直线AA上，
∵点B ，B ，B ，……都在直线y＝x，AO＝2
∴直线AA 的解析式为y＝x＋2，
∴y＝×＋2＝3
∴A（，3）
同理可得：A的横坐标为：2
y＝×2＋2＝4
∴A （2，4）
∴A（3，5）
……
∴An（n，n+2），
∴A2019（2019，2021），
故答案为：（2019，2021）．
练习册系列答案
相关题目
【题目】在方格纸中，每个方格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形.如图甲中，每个小正方形的边长为1，以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化．
（1）根据图甲，填写下表，并计算出格点三角形面积的平均值；
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
（2）在图乙中，所给的方格纸大小与图甲一样，如果以线段CD为一边，作格点三角形，试填写下表，并计算出格点三角形面积的平均值；
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
（3）如果将图乙中格点三角形面积记为s，频数记为x，根据你所填写的数据，猜测s与x之间存在哪种函数关系，并求出函数关系式．
