题目内容
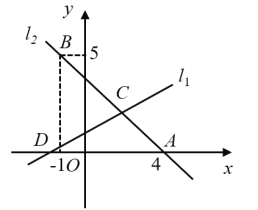
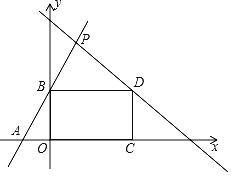
【题目】如图所示，在平面直角坐标系中，直线y1＝2x+4分别与x轴，y轴交于A，B两点，以线段OB为一条边向右侧作矩形OCDB，且点D在直线y2＝﹣x+b上，若矩形OCDB的面积为20，直线y1＝2x+4与直线y2＝﹣x+b交于点P．则P的坐标为（ ）
A.（2，8）B.
C.
D.（4，12）
【答案】C
【解析】
由直线y1=2x+4求得OB=4，根据解析式面积求得D(5，4)，代入y2=-x+b求得解析式，然后联立解析式，解方程组即可求得．
∵直线y1=2x+4分别与x轴，y轴交于A，B两点，
∴B(0，4)，
∴OB=4，
∵矩形OCDB的面积为20，
∴OBOC=20，
∴OC=5，
∴D(5，4)，
∵D在直线y2=﹣x+b上，
∴4=﹣5+b，
∴b=9，
∴直线y2=-x+9，
解
得
，
∴P(
，
)，
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
