题目内容
14.计算:(1)$\sqrt{45}$÷3$\sqrt{\frac{1}{5}}$×$\frac{3}{2}$$\sqrt{5}$
(2)($\sqrt{27}$-$\sqrt{24}$+2$\sqrt{12}$)÷2$\sqrt{3}$
(3)($\frac{1}{3}$$\sqrt{1\frac{1}{4}}$)×$\sqrt{(-\sqrt{27})^{2}}$×$\sqrt{1.6}$.
分析 (1)根据二次根式的除法法则和乘法法则求解;
(2)先进行二次根式的化简,然后进行除法运算,最后合并;
(3)先进行二次根式的乘法运算,然后合并化简.
解答 解:(1)原式=5×$\frac{3}{2}$$\sqrt{5}$
=$\frac{15\sqrt{5}}{2}$;
(2)原式=(3$\sqrt{3}$-2$\sqrt{6}$+4$\sqrt{3}$)÷2$\sqrt{3}$
=$\frac{7}{2}$-$\sqrt{2}$;
(3)原式=($\frac{1}{3}$$\sqrt{\frac{5}{4}}$)×3$\sqrt{3}$×$\frac{2\sqrt{10}}{5}$
=$\frac{\sqrt{15}}{2}$×$\frac{2\sqrt{10}}{5}$
=$\sqrt{6}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的乘法法则和除法法则以及二次根式的化简.

练习册系列答案
相关题目
3.若$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{7}$,且a-b+c=12,则2a-3b+c等于( )
| A. | $\frac{3}{7}$ | B. | 2 | C. | 4 | D. | 12 |
 如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.
如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.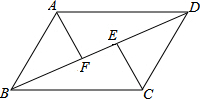 如图,在?ABCD中,点E、F分别是对角线BD上两点,且BF=DE,连接AF、CE.求证:四边形AFCE是平行四边形.
如图,在?ABCD中,点E、F分别是对角线BD上两点,且BF=DE,连接AF、CE.求证:四边形AFCE是平行四边形.