题目内容
15.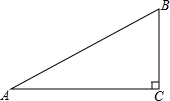 如图,在Rt△ACB中,∠ACB=90°
如图,在Rt△ACB中,∠ACB=90°(1)用尺规在AC边上求作点D,使AD=BD(保留痕迹,不谢作法);
(2)若(1)中所得BD平分∠ABC,则tanA=$\frac{1}{2}$(直接写出结果)
分析 (1)作出线段AB的垂直平分线进而得出其与AC的交点D即可;
(2)利用角平分线的性质以及线段垂直平分线的性质得出∠A=∠ABD=∠CBD=30°,进而得出答案.
解答  解:(1)如图所示:D点即为所求;
解:(1)如图所示:D点即为所求;
(2)∵(1)中所得BD平分∠ABC,
∴∠ABD=∠CBD,
∵AD=BD,
∴∠A=∠DBA,
∴∠A=∠ABD=∠CBD=30°,
则sinA=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了复杂作图以及等腰三角形和线段垂直平分线的性质,得出∠A=∠ABD=∠CBD=30°是解题关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
5.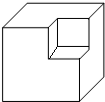 从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
 从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )
从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,得到一个如图所示的几何体,则该几何体的体积是( )| A. | 4a3 | B. | 8a3 | C. | 56a3 | D. | 58a3 |
6.温度-4℃比-9℃高( )
| A. | -5℃ | B. | 5℃ | C. | -13℃ | D. | 13℃ |
3.若|a-3|-3+a=0,则a的取值范围是( )
| A. | a≤3 | B. | a<3 | C. | a=3 | D. | a≥3 |
7.若x=2y-3,则(x-2y)2-3x+6y的值是( )
| A. | -18 | B. | 0 | C. | 9 | D. | 18 |
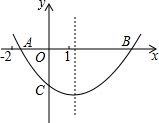 二次函数y=ax2+bx+c的图象如图所示,OA=OC,则下列结论:
二次函数y=ax2+bx+c的图象如图所示,OA=OC,则下列结论: