Question

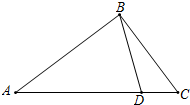如图，在Rt△ABC中，∠ABC=90°，AB=16，BC=12，点D为AC边上的动点，点D从点C出发，沿边CA往A运动，当运动到点A时停止，若设点D运动的时间为t秒，点D运动的速度为每秒2个单位长度．
（1）当t=2时，CD=

 

，AD=

 

；（请直接写出答案）
（2）当t=

 

时，△CBD是直角三角形；（请直接写出答案）
（3）求当t为何值时，△CBD是等腰三角形？并说明理由．

Answer 1

考点：勾股定理的逆定理,等腰三角形的判定

专题：动点型

分析：（1）根据CD=速度×时间列式计算即可得解，利用勾股定理列式求出AC，再根据AD=AC-CD代入数据进行计算即可得解；
（2）分①∠CDB=90°时，利用△ABC的面积列式计算即可求出BD，然后利用勾股定理列式求解得到CD，再根据时间=路程÷速度计算；②∠CBD=90°时，点D和点A重合，然后根据时间=路程÷速度计算即可得解；
（3）分①CD=BD时，过点D作DE⊥BC于E，根据等腰三角形三线合一的性质可得CE=BE，从而得到CD=AD；②CD=BC时，CD=12；③BD=BC时，过点B作BF⊥AC于F，根据等腰三角形三线合一的性质可得CD=2CF，再由（2）的结论解答．

解答：解：（1）t=2时，CD=2×2=4，
∵∠ABC=90°，AB=16，BC=12，
∴AC=

AB2+BC2

=

162+122

=20，
∴AD=AC-CD=20-4=16；

（2）①∠CDB=90°时，S_△ABC=

1

2

AC•BD=

1

2

AB•BC，
即

1

2

×20•BD=

1

2

×16×12，
解得BD=9.6，
所以CD=

BC2-BD2

=

122-9．62

=7.2，
t=7.2÷2=3.6秒；
②∠CBD=90°时，点D和点A重合，
t=20÷2=10秒，
综上所述，t=3.6或10秒；
故答案为：（1）4，16；（2）3.6或10秒；

（3）①CD=BD时，如图1，过点D作DE⊥BC于E，
则CE=BE，
∴CD=AD=

1

2

AC=

1

2

×20=10，
t=10÷2=5；
②CD=BC时，CD=12，t=12÷2=6；
③BD=BC时，如图2，过点B作BF⊥AC于F，
则CF=7.2，
CD=2CF=7.2×2=14.4，
∴t=14.4÷2=7.2，
综上所述，t=5秒或6秒或7.2秒时，△CBD是等腰三角形．

点评：本题考查了勾股定理，等腰三角形的判定与性质，三角形的面积，（2）（3）难点在于要分情况讨论，作出图形更形象直观．