Question

13．一条抛物线经过A（1，0），B（3，0），C（0，3）三点，其顶点为D，则△DBC的面积=（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 由待定系数法将A（-4，0），B（0，-4），C（2，0）三个点的坐标代入y=ax²+bx+c，联立求解即可得出函数解析式，进一步求得顶点坐标，利用三角形的面积得出答案即可．

解答 解：∵抛物线经过A（1，0），B（3，0），
∴设抛物线的解析式为y=a（x-1）（x-3），
把C（0，3）代入得，3=a×（0-1）（0-3），解得a=1，
∴抛物线的解析式为：y=（x-1）（x-3），即y=x²-4x+3=（x-2）²-1，
顶点D坐标为（2，-1），
如图，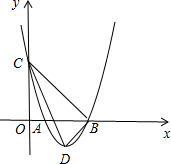

∴△DBC的面积为S=$\frac{1}{2}$×3×3+$\frac{1}{2}$（2+3）×1-$\frac{1}{2}$×2×（3+1）=4．
故选D．

点评 此题考查待定系数法求函数解析式，图形面积的求法，掌握待定系数法求函数解析式的方法与步骤是解决问题的关键．