题目内容
16.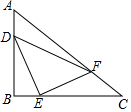 如图,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、E、F分别是边AB、BC、AC上的动点,则DE+EF+FD的最小值为( )
如图,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、E、F分别是边AB、BC、AC上的动点,则DE+EF+FD的最小值为( )| A. | 4.8 | B. | 6 | C. | 10 | D. | 无法确定 |
分析 如图作F关于直线AB的对称点M,作F关于直线BC的对称点N,连接MN,DM,EF,EN,由DF+DE+EF=DM+DE+EN,可知当D、E、M、N共线时,且BF⊥AC时,DE+EF+FD的值最小,最小值=2BF,求出BF的值即可解决问题.
解答 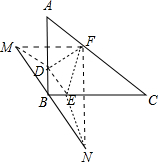 解:如图作F关于直线AB的对称点M,作F关于直线BC的对称点N,连接MN,DM,EF,EN,
解:如图作F关于直线AB的对称点M,作F关于直线BC的对称点N,连接MN,DM,EF,EN,
∵DF+DE+EF=DM+DE+EN,
∵DM+DE+EN≥MN,
∴当D、E、M、N共线时,且BF⊥AC时,DE+EF+FD的值最小,最小值=2BF,
∵BF⊥AC,
∴$\frac{1}{2}$•AC•BF=$\frac{1}{2}$•AB•AC,
∴BF=$\frac{AB•BC}{AC}$=$\frac{12}{5}$=2.4,
∴DE+EF+FD的最小值为4.8.
故选A.
点评 本题考查轴对称-最短问题、两点之间线段最短、垂线段最短等知识,解题的关键是灵活运用轴对称以及垂线段最短解决最短问题,属于中考选择题中的压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在$\sqrt{3}$,$\frac{1}{2}$,0,-2这四个数中,为无理数的是( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
11.班上有男女生共41人,女生人数的一半比男生总数少8人,该班女生人数是( )
| A. | 20人 | B. | 21人 | C. | 22人 | D. | 23人 |
8.用A、B两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如表:
(1)若要配制这种饮料10千克,要求至少含有4000单位的维生素C,试求出所需A种原料最少多少千克?
(2)如要求购买A、B两种原料的费用不超过52元,试求出所需A种原料最多多少千克?
| 原料 维生素及价格 | A种原料 | B种原料 |
| 维生素C(单位/千克) | 600 | 100 |
| 原料价格(元/千克) | 6 | 4 |
(2)如要求购买A、B两种原料的费用不超过52元,试求出所需A种原料最多多少千克?
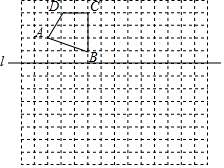 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和直线l,按要求画图.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和直线l,按要求画图.