题目内容
19. 小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形的高CD长度为10厘米,由此就可求得半径解决问题.请你帮小明:
小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形的高CD长度为10厘米,由此就可求得半径解决问题.请你帮小明:(1)用尺规作图找出圆心;
(2)算一下这个圆的半径是多少厘米.
分析 (1)根据垂径定理找出AC、BC的垂直平分线,两直线的交点即为所求;
(2)根据题意,已知弦AB的长60,AD=30,CD=10,根据勾股定理和垂径定理可以求得圆的半径.
解答 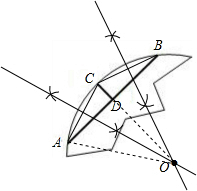 解:(1)作图找圆心O:
解:(1)作图找圆心O:
①连接AC、BC,
②作AC、BC的垂直平分线交点为O,
O点就是求作的圆心;
(2)设此圆的半径为r厘米,连结DO、AO,
可得OD=(r-10)cm.
由题意,得AD=30厘米
∴r2=302+(r-10)2,
解得 r=50,
答:这个圆的半径是50厘米.
点评 本题考查了垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+($\frac{a}{2}$)2成立,知道这三个量中的任意两个,就可以求出另外一个.

练习册系列答案
相关题目
9.一次函数y=kx+b经过第一、三、四象限,则下列正确的是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
11.已知⊙O的半径为3cm,点P是直线l上一点,OP的长为4cm,则直线l与⊙O的位置关系是( )
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种都有可能 |
8.方程组$\left\{\begin{array}{l}{2x-y=5}\\{x-2y=1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
 在如图的直角坐标系中,已知点A(1,0);B(0,-2),将线段AB绕点A按逆时针方向旋转90°至AC.
在如图的直角坐标系中,已知点A(1,0);B(0,-2),将线段AB绕点A按逆时针方向旋转90°至AC.
 用等分圆周的方法画下列图形.
用等分圆周的方法画下列图形. (1)如图,六边形ABCDEF满足:AB$\stackrel{∥}{=}$EF,AF$\stackrel{∥}{=}$CD.仅用无刻度的直尺画出一条直线l,使得直线l能将六边形ABCDEF的面积给平分;
(1)如图,六边形ABCDEF满足:AB$\stackrel{∥}{=}$EF,AF$\stackrel{∥}{=}$CD.仅用无刻度的直尺画出一条直线l,使得直线l能将六边形ABCDEF的面积给平分;