题目内容
4.下列运算中,正确的是( )| A. | $\sqrt{4}$=±2 | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{a^2}=a$ | D. | 4的平方根是±2 |
分析 A、$\sqrt{4}$表示4的算术平方根,值为2;
B、不是同类二次根式,不能合并;
C、没说明a的取值,结果只能为|a|;
D、4的平方根是±2.
解答 解:A、$\sqrt{4}$=2,所以此选项不正确;
B、$\sqrt{2}+\sqrt{3}$不能合并同类项,所以此选项不正确;
C、$\sqrt{{a}^{2}}$=|a|,所以此选项不正确;
D、4的平方根是±2,所以此选项正确;
故选D.
点评 本题主要考查了平方根算术平方根概念的运用.如果x2=a(a≥0),则x是a的平方根.若a>0,则它有两个平方根,我们把正的平方根叫a的算术平方根;若a=0,则它有一个平方根,即0的平方根是0,0的算术平方根也是0,负数没有平方根.

练习册系列答案
相关题目
15.下列计算中,正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{5}+\sqrt{6}=\sqrt{11}$ | C. | $2+\sqrt{2}=2\sqrt{2}$ | D. | $\sqrt{2}+\sqrt{2}=2\sqrt{2}$ |
19.下列实数:$\sqrt{11}$、3.14、$\frac{1}{7}$、π、$\sqrt{9}$,其中无理数的个数有( )
| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
9.下列命题中的假命题是( )
| A. | 对顶角相等 | |
| B. | 内错角相等,两直线互相平行 | |
| C. | 同位角相等 | |
| D. | 平行于同一条直线的两直线互相平行 |
16.已知平行四边形的一组邻边分别为a、b,且a边上的高为h,那么b边上的高为( )
| A. | $\frac{ah}{b}$ | B. | $\frac{ab}{h}$ | C. | $\frac{bh}{a}$ | D. | abh |
13. 如图,在四边形ABCD中,BE⊥AC于点E,连接DE,四边形ABCD的面积为12cm2.若BE平分∠ABC,则四边形ABED的面积为( )
如图,在四边形ABCD中,BE⊥AC于点E,连接DE,四边形ABCD的面积为12cm2.若BE平分∠ABC,则四边形ABED的面积为( )
 如图,在四边形ABCD中,BE⊥AC于点E,连接DE,四边形ABCD的面积为12cm2.若BE平分∠ABC,则四边形ABED的面积为( )
如图,在四边形ABCD中,BE⊥AC于点E,连接DE,四边形ABCD的面积为12cm2.若BE平分∠ABC,则四边形ABED的面积为( )| A. | 4cm2 | B. | 6cm2 | C. | 8cm2 | D. | 10cm2 |
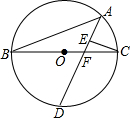 如图,BC为⊙O的直径,AB为⊙O的弦,D为$\widehat{BC}$的中点,CE⊥AD于E,AD交BC于点F,tan∠B=$\frac{1}{2}$
如图,BC为⊙O的直径,AB为⊙O的弦,D为$\widehat{BC}$的中点,CE⊥AD于E,AD交BC于点F,tan∠B=$\frac{1}{2}$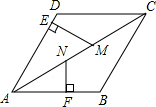 如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN的长度为4.
如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN的长度为4.