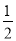题目内容
如图,已知二次函数y=﹣x2+bx+c(其中b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标.
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
(3)沿直线AC方向平移该二次函数图象,使得CM与平移前的CB相等,求平移后点M的坐标.
(4)点P是直线AC上的动点,过点P作直线AC的垂线PQ,记点M关于直线PQ的对称点为M′.当以点P、A、M、M′为顶点的四边形为平行四边形时,直接写出点P的坐标.
练习册系列答案
相关题目
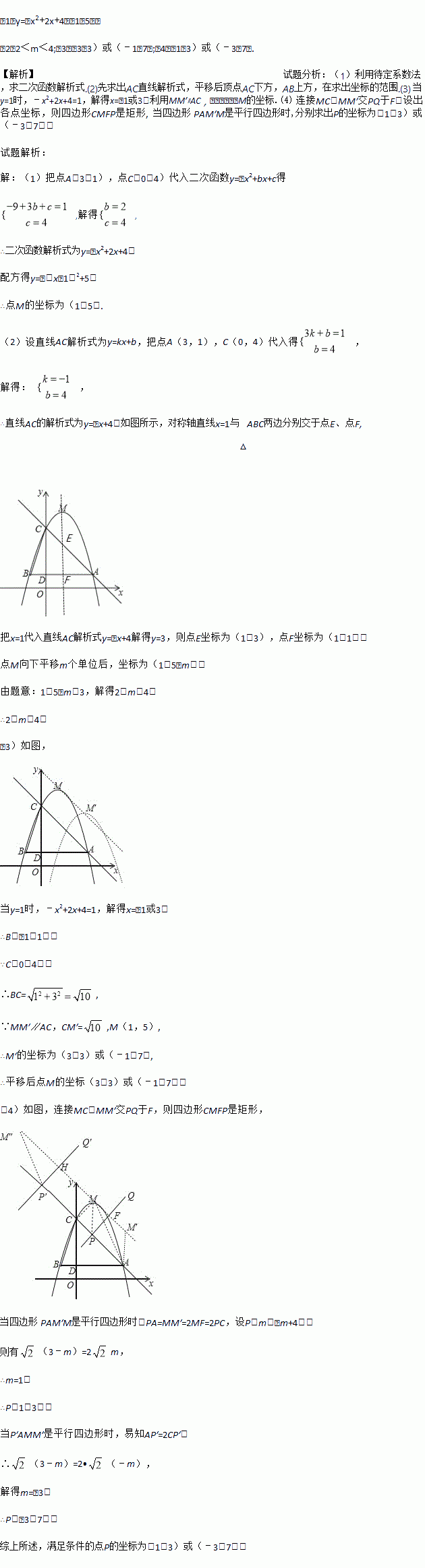

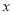 的一元二次方程
的一元二次方程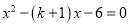 的一个根是2,则
的一个根是2,则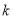 的值为( )
的值为( )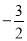 B.
B. 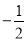 C. 0 D. -2
C. 0 D. -2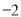 ,
, 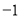 ,0,1,2,3这6个数中任取一个数记作
,0,1,2,3这6个数中任取一个数记作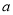 ,放回去,再从这六个数中任意取一个数记作
,放回去,再从这六个数中任意取一个数记作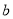 ,则使得分式方程
,则使得分式方程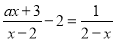 有整数解,且使得函数
有整数解,且使得函数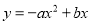 的图象经过第一三四象限的所有
的图象经过第一三四象限的所有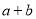 的值有( ).
的值有( ).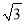 ≈1.73,结果保留整数)
≈1.73,结果保留整数)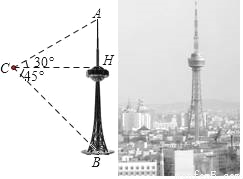
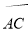 的长为_____.
的长为_____.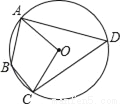
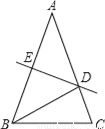
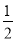 的相反数是( )
的相反数是( )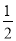 B. 2 C. -2 D. -
B. 2 C. -2 D. -