题目内容
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() .
.

(1)![]() 点的坐标为( , ),
点的坐标为( , ),![]() 点的坐标为( , );
点的坐标为( , );
(2)如图1,已知直线![]() 经过点
经过点![]() 和
和![]() 轴上一点
轴上一点![]() ,
,![]() ,点
,点![]() 在直线AB上且位于
在直线AB上且位于![]() 轴右侧图象上一点,连接
轴右侧图象上一点,连接![]() ,且
,且![]()
![]() .
.
①求![]() 点坐标;
点坐标;
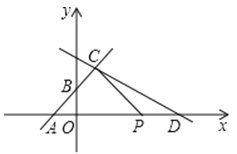
②将![]() 沿直线AM 平移得到
沿直线AM 平移得到![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合,
重合,![]() 为
为![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出最小值及此时 N 点的坐标;
的值最小时,请求出最小值及此时 N 点的坐标;
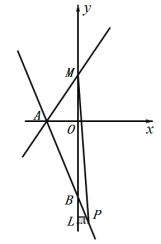
(3)如图 2,将点![]() 向左平移 2 个单位到点
向左平移 2 个单位到点![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,直线
轴的对称点,直线![]() 经过点
经过点![]() 和点
和点![]() ,动点
,动点![]() 从原点出发沿着
从原点出发沿着![]() 轴正方向运动,连接
轴正方向运动,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出![]() 点坐标.
点坐标.
【答案】(1)-1,0;0,-3;(2)①点![]() ;②点
;②点![]() ,最小值为
,最小值为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据两个非负数和为0的性质即可求得点A、B的坐标;
(2)①先求得直线AB的解析式,根据![]() 求得
求得![]() ,继而求得点
,继而求得点![]() 的横坐标,从而求得答案;
的横坐标,从而求得答案;
②先求得直线AM的解析式及点![]() 的坐标,过点
的坐标,过点![]() 过
过![]() 轴的平行线交直线
轴的平行线交直线![]() 与点
与点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 的延长线于点
的延长线于点![]() ,求得
,求得![]() ,即
,即![]() 为最小值,即点
为最小值,即点![]() 为所求,求得点
为所求,求得点![]() 的坐标,再求得
的坐标,再求得![]() 的长即可;
的长即可;
(3)先求得直线BD的解析式,设点![]() ,同理求得直线
,同理求得直线![]() 的解析式,求出点
的解析式,求出点![]() 的坐标为
的坐标为![]() ,证得
,证得![]() ,分∠QGE为直角、∠EQG为直角、∠QEG为直角,三种情况分别求解即可.
,分∠QGE为直角、∠EQG为直角、∠QEG为直角,三种情况分别求解即可.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,
故点A、B的坐标分别为:![]() ,
,
故答案为:![]() ;
;![]() ;
;
(2)①直线![]() 经过点
经过点![]() 和
和![]() 轴上一点
轴上一点![]() ,
,![]() ,
,
∴![]() ,
,
由(1)得:点A、B的坐标分别为:![]() ,则
,则![]() ,
,![]() ,
,
设直线AB的解析式为:![]() ,
,
∴![]()
解得:![]()
∴直线AB的解析式为:![]() ,
,
∵![]()
∴![]()
作![]() ⊥
⊥![]() 轴于
轴于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的横坐标为
的横坐标为![]() ,
,
又点![]() 在直线AB上,
在直线AB上,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
②由(1)得:点A、B的坐标分别为:![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
设直线AM的解析式为:![]() ,
,
∴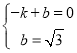
解得: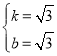
∴直线AM的解析式为:![]() ,
,
根据题意,平移后点![]() ,
,
过点![]() 过
过![]() 轴的平行线交直线
轴的平行线交直线![]() 与点
与点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 的延长线于点
的延长线于点![]() ,如图1,
,如图1,
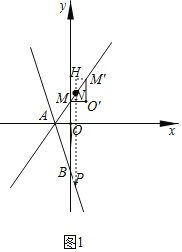
∴![]() ∥
∥![]() ,
,
∵![]() ,
,
∴![]() ,
,
则![]() ,
,
![]() 为最小值,即点
为最小值,即点![]() 为所求,
为所求,
则点N的横坐标与点![]() 的横坐标相同都是
的横坐标相同都是![]() ,
,
点N在直线AM上,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为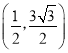 ,
,
∴![]() ,
,
![]() ;
;
(3)根据题意得:
点![]() 的坐标分别为:
的坐标分别为:![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴直线BD的解析式为:![]() ,
,
设点![]() ,同理直线
,同理直线![]() 的解析式为:
的解析式为:![]() ,
,
∵![]() ,
,
∴设直线![]() 的解析式为:
的解析式为:![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
则直线![]() 的解析式为:
的解析式为:![]() ,
,
故点![]() 的坐标为
的坐标为![]() ,
,
即![]() ,
,
①当![]() 为直角时,
为直角时,
如下图,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
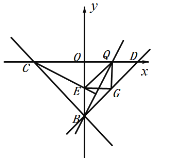
则点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 的坐标代入直线
的坐标代入直线![]() 的解析式
的解析式![]() 并解得:
并解得:![]() ,
,
故点![]() ;
;
②当![]() 为直角时,
为直角时,
如下图,作![]() 于
于![]() ,
,
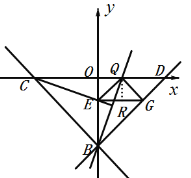
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ∥
∥![]() 轴,
轴,![]() 、
、![]() 和
和![]() 都是底边相等的等腰直角三角形,
都是底边相等的等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 的坐标代入直线
的坐标代入直线![]() 的解析式
的解析式![]() 并解得:
并解得:![]() ,
,
故点![]() ;
;
③当![]() 为直角时,
为直角时,
如下图,
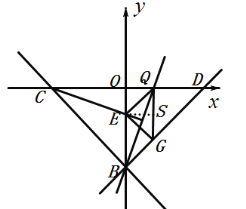
同理可得点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 的坐标代入直线
的坐标代入直线![]() 的解析式
的解析式![]() 并解得:
并解得:![]() ,
,
故点![]() ;
;
综上,点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() .
.

 计算高手系列答案
计算高手系列答案【题目】某校兴趣小组在创客嘉年华活动中组织了计算机编程比赛,八年级每班派25名学生参加,成绩分别为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
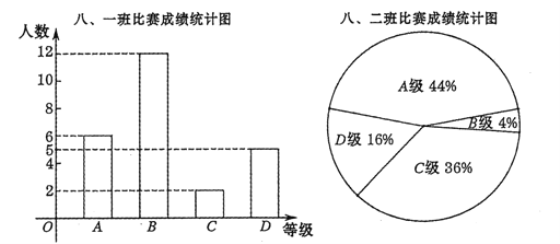
班级 | 平均数(分) | 中位数(分) | 众数(分) | 方差 |
一班 | 8.76 | 9 | 9 |
|
二班 | 8.76 | 8 | 10 |
|
请根据本学期所学过的《数据的分析》相关知识分析上述数据,帮助计算机编程老师选择一个班级参加校级比赛,并阐述你选择的理由.