题目内容
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 上两点,且
上两点,且![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.

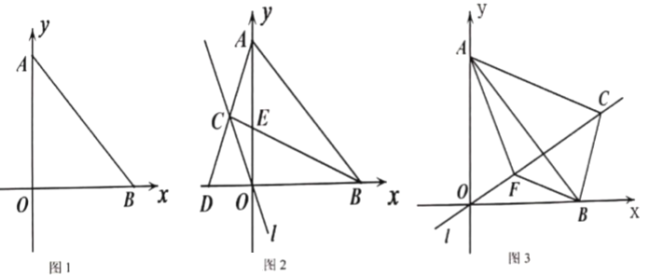
(1)如图1,当![]() 两点重合时,求证:
两点重合时,求证:![]() ;
;
(2)延长![]() 与
与![]() 交于点
交于点![]() .
.
①如图2,求证:![]() ;
;
②如图3,连接![]() ,若
,若![]() ,则
,则![]() 的面积为______________.
的面积为______________.
【答案】(1)见解析;(2)①见解析;②2.
【解析】
(1)当D、E两点重合时,则AD=CD,然后由等边三角形的性质可得∠CBD的度数,根据等腰三角形的性质和三角形的外角性质可得∠F的度数,于是可得∠CBD与∠F的关系,进而可得结论;
(2)①过点E作EH∥BC交AB于点H,连接BE,如图4,则易得△AHE是等边三角形,根据等边三角形的性质和已知条件可得EH=CF,∠BHE=∠ECF=120°,BH=EC,于是可根据SAS证明△BHE≌△ECF,可得∠EBH=∠FEC,易证△BAE≌△BCD,可得∠ABE=∠CBD,从而有∠FEC=∠CBD,然后根据三角形的内角和定理可得∠BGE=∠BCD,进而可得结论;
②易得∠BEG=90°,于是可知△BEF是等腰直角三角形,由30°角的直角三角形的性质和等腰直角三角形的性质易求得BE和BF的长,过点E作EM⊥BF于点F,过点C作CN⊥EF于点N,如图5,则△BEM、△EMF和△CFN都是等腰直角三角形,然后利用等腰直角三角形的性质和30°角的直角三角形的性质可依次求出BM、MC、CF、FN、CN、GN的长,进而可得△GCN也是等腰直角三角形,于是有∠BCG=90°,故所求的△BCG的面积=![]() ,而BC和CG可得,问题即得解决.
,而BC和CG可得,问题即得解决.
解:(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,
当D、E两点重合时,则AD=CD,∴![]() ,
,
∵![]() ,∴∠F=∠CDF,
,∴∠F=∠CDF,
∵∠F+∠CDF=∠ACB=60°,∴∠F=30°,
∴∠CBD=∠F,∴![]() ;
;
(2)①∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC,
过点E作EH∥BC交AB于点H,连接BE,如图4,则∠AHE=∠ABC=60°,∠AEH=∠ACB=60°,
∴△AHE是等边三角形,∴AH=AE=HE,∴BH=EC,
∵![]() ,CD=CF,∴EH=CF,
,CD=CF,∴EH=CF,
又∵∠BHE=∠ECF=120°,∴△BHE≌△ECF(SAS),
∴∠EBH=∠FEC,EB=EF,
∵BA=BC,∠A=∠ACB=60°,AE=CD,
∴△BAE≌△BCD(SAS),∴∠ABE=∠CBD,∴∠FEC=∠CBD,
∵∠EDG=∠BDC,∴∠BGE=∠BCD=60°;

②∵∠BGE=60°,∠EBD=30°,∴∠BEG=90°,
∵EB=EF,∴∠F=∠EBF=45°,
∵∠EBG=30°,BG=4,∴EG=2,BE=2![]() ,
,
∴BF=![]() ,
,![]() ,
,
过点E作EM⊥BF于点F,过点C作CN⊥EF于点N,如图5,则△BEM、△EMF和△CFN都是等腰直角三角形,
∴![]() ,
,
∵∠ACB=60°,∴∠MEC=30°,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∴∠GCF=90°=∠GCB,
,∴∠GCF=90°=∠GCB,
∴![]() ,
,
∴△BCG的面积=![]() .
.
故答案为:2.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案【题目】甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图.
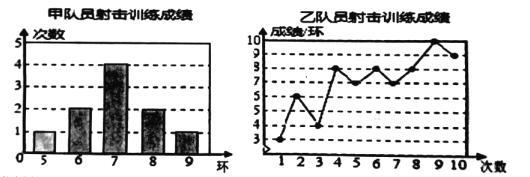
并整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?