ЬтФПФкШн
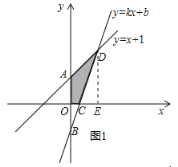
ЁОЬтФПЁПШчЭМЃЌвбжЊКЏЪ§ y=x+1 ЕФЭМЯѓгы y жсНЛгкЕу AЃЌвЛДЮКЏЪ§ y=kx+b ЕФЭМЯѓОЙ§Еу BЃЈ0ЃЌЉ1ЃЉЃЌгыx жс вдМА y=x+1 ЕФЭМЯѓЗжБ№НЛгкЕу CЁЂDЃЌЧвЕу D ЕФзјБъЮЊЃЈ1ЃЌnЃЉЃЌ

ЃЈ1ЃЉдђn= ЃЌk= ЃЌb= ЃЛ
ЃЈ2ЃЉКЏЪ§ y=kx+b ЕФКЏЪ§жЕДѓгкКЏЪ§ y=x+1 ЕФКЏЪ§жЕЃЌдђXЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЃЈ3ЃЉЧѓЫФБпаЮ AOCD ЕФУцЛ§ЃЛ
ЃЈ4ЃЉдк xжсЩЯЪЧЗёДцдкЕу PЃЌЪЙЕУвдЕу PЃЌCЃЌD ЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЧѓГіЕу P ЕФзјБъЃЛ ШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЌ3ЃЌ-1ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЈ4ЃЉ
ЃЈ4ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЖдгкжБЯп![]() ЃЌСю
ЃЌСю![]() ЧѓГі
ЧѓГі![]() ЕФжЕЃЌШЗЖЈГіAЕФзјБъЃЌАбBзјБъДњШы
ЕФжЕЃЌШЗЖЈГіAЕФзјБъЃЌАбBзјБъДњШы![]() жаЧѓГіbЕФжЕЃЌдйНЋDзјБъДњШы
жаЧѓГіbЕФжЕЃЌдйНЋDзјБъДњШы![]() ЧѓГіnЕФжЕЃЌНјЖјНЋDзјБъДњШыЧѓГі
ЧѓГіnЕФжЕЃЌНјЖјНЋDзјБъДњШыЧѓГі![]() ЕФжЕМДПЩЃЛ
ЕФжЕМДПЩЃЛ
гЩСНИівЛДЮКЏЪ§НтЮіЪНЃЌНсКЯЭМЯѓШЗЖЈГі![]() ЕФЗЖЮЇЃЛ
ЕФЗЖЮЇЃЛ
Й§Dзї![]() ДЙжБгк
ДЙжБгк![]() жсЃЌЫФБпаЮ
жсЃЌЫФБпаЮ![]() ЕФУцЛ§ЕШгкЬнаЮ
ЕФУцЛ§ЕШгкЬнаЮ![]() УцЛ§МѕШЅШ§НЧаЮ
УцЛ§МѕШЅШ§НЧаЮ![]() УцЛ§ЃЌЧѓГіМДПЩЃЛ
УцЛ§ЃЌЧѓГіМДПЩЃЛ
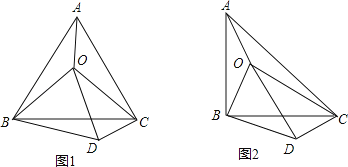
дк![]() жсЩЯДцдкЕуPЃЌЪЙЕУвдЕуPЁЂCЁЂDЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌРэгЩЃКЗжСНжжЧщПіПМТЧЃК
жсЩЯДцдкЕуPЃЌЪЙЕУвдЕуPЁЂCЁЂDЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌРэгЩЃКЗжСНжжЧщПіПМТЧЃК![]() ЃЛ
ЃЛ![]() ЃЌЗжБ№ЧѓГіPЕузјБъМДПЩЃЎ
ЃЌЗжБ№ЧѓГіPЕузјБъМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЖдгкжБЯп![]() ЃЌСю
ЃЌСю![]() ЕУЕН
ЕУЕН![]() ЃЌМДAЃЈ0ЃЌ1ЃЉЃЌАбBЃЈ0ЃЌ-1ЃЉДњШы
ЃЌМДAЃЈ0ЃЌ1ЃЉЃЌАбBЃЈ0ЃЌ-1ЃЉДњШы![]() жаЃЌЕУЃК
жаЃЌЕУЃК![]() ЃЌАбDЃЈ1ЃЌnЃЉДњШы
ЃЌАбDЃЈ1ЃЌnЃЉДњШы![]() ЕУЃК
ЕУЃК![]() ЃЌМДDЃЈ1ЃЌ2ЃЉЃЌАбDзјБъДњШы
ЃЌМДDЃЈ1ЃЌ2ЃЉЃЌАбDзјБъДњШы![]() жаЕУЃК
жаЕУЃК![]() ЃЌМД
ЃЌМД![]() ЃЌЙЪД№АИЮЊЃК2ЃЌ3ЃЌ-1ЃЛ
ЃЌЙЪД№АИЮЊЃК2ЃЌ3ЃЌ-1ЃЛ
вЛДЮКЏЪ§![]() гы
гы![]() НЛгкЕуDЃЈ1ЃЌ2ЃЉЃЌгЩЭМЯѓЕУЃККЏЪ§
НЛгкЕуDЃЈ1ЃЌ2ЃЉЃЌгЩЭМЯѓЕУЃККЏЪ§![]() ЕФКЏЪ§жЕДѓгкКЏЪ§
ЕФКЏЪ§жЕДѓгкКЏЪ§![]() ЕФКЏЪ§жЕ
ЕФКЏЪ§жЕ![]() ЪБЕФШЁжЕЗЖЮЇЪЧ
ЪБЕФШЁжЕЗЖЮЇЪЧ![]() ЃЛЙЪД№АИЮЊЃК
ЃЛЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
Й§Dзї![]() ДЙжБгк
ДЙжБгк![]() жсЃЌШчЭМ1ЫљЪОЃЌдђ
жсЃЌШчЭМ1ЫљЪОЃЌдђ![]()
![]()
![]()
ЃЈ4ЃЉШчЭМ2ЃЌдк![]() жсЩЯДцдкЕуPЃЌЪЙЕУвдЕуPЁЂCЁЂDЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌРэгЩЃКЗжСНжжЧщПіПМТЧЃКЕБ
жсЩЯДцдкЕуPЃЌЪЙЕУвдЕуPЁЂCЁЂDЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌРэгЩЃКЗжСНжжЧщПіПМТЧЃКЕБ![]() ЪБЃЌПЩЕУ
ЪБЃЌПЩЕУ![]()
![]() аБТЪЮЊ3ЃЌ
аБТЪЮЊ3ЃЌ![]() аБТЪЮЊ
аБТЪЮЊ![]() ЃЌ
ЃЌ![]()
![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]() Сю
Сю![]() МД
МД![]() ЕБ
ЕБ![]() ЪБЃЌгЩDКсзјБъЮЊ1ЃЌЕУЕНPЕуКсзјБъЮЊ1ЃЌ
ЪБЃЌгЩDКсзјБъЮЊ1ЃЌЕУЕНPЕуКсзјБъЮЊ1ЃЌ![]() дк
дк![]() жсЩЯЃЌ
жсЩЯЃЌ![]()