题目内容
11. 如图,在扇形ACB中,∠ACB=90°,BC为直径作半圆,圆心为O.过点O作AC的平行线交两弧于点D、E,若BC=2,则阴影部分的面积是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.
如图,在扇形ACB中,∠ACB=90°,BC为直径作半圆,圆心为O.过点O作AC的平行线交两弧于点D、E,若BC=2,则阴影部分的面积是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.
分析 如图,连接CE.图中S阴影=S扇形BCE-S扇形BOD-S△OCE.根据已知条件易求得OB=OC=OD=1,BC=CE=2.∠ECB=60°,OE=$\sqrt{3}$,所以由扇形面积公式、三角形面积公式进行解答即可.
解答 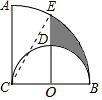 解:如图,连接CE.
解:如图,连接CE.
∵AC⊥BC,AC=BC=2,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,
∴∠ACB=90°,OB=OC=OD=1,BC=CE=2.
又∵OE∥AC,
∴∠ACB=∠COE=90°.
∴在直角△OEC中,OC=1,CE=2,
∴∠CEO=30°,∠ECB=60°,OE=$\sqrt{3}$,
∴S阴影=S扇形BCE-S扇形BOD-S△OCE=$\frac{60π•{2}^{2}}{360}$-$\frac{1}{4}$π×12-$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{2}{3}$π-$\frac{1}{4}$π-$\frac{\sqrt{3}}{2}$=$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.
点评 本题考查了扇形面积的计算.不规则图形的面积一定要注意分割成规则图形的面积进行计算.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
2.2016年鄞州区财政收入仍保持持续增长态势,全年财政收入为373.9亿元,其中373.9亿元用科学记数法表示为( )
| A. | 373.9×108元 | B. | 37.39×109元 | C. | 3.739×1010元 | D. | 0.3739×1011 |
19.已知248-1可以被在60~70之间的两个整数整除,则这两个数是( )
| A. | 64,63 | B. | 61,65 | C. | 61,67 | D. | 63,65 |
20. 如图所示的几何体三视图的主视图是( )
如图所示的几何体三视图的主视图是( )
 如图所示的几何体三视图的主视图是( )
如图所示的几何体三视图的主视图是( )| A. |  | B. |  | C. |  | D. |  |
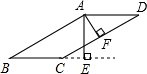 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,点E,F为垂足,∠EAF=30°,AE=3cm,AF=2cm,求平行四边形ABCD的周长.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,点E,F为垂足,∠EAF=30°,AE=3cm,AF=2cm,求平行四边形ABCD的周长.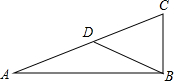 如图,已知在△ABC中,AB=12,BC=5,AC=13,D为AC的中点,连接BD,求BD的长度.
如图,已知在△ABC中,AB=12,BC=5,AC=13,D为AC的中点,连接BD,求BD的长度.