题目内容
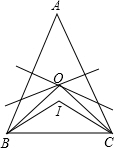如图点O是△ABC的边AB、AC的中垂线的交点，I是∠ABC、∠ACB的平分线的交点，且∠I+∠BOC=180°，求∠BAC的度数．
解：由中垂线的性质得：∠OBA+∠OCA=∠A，
∴∠BOC=180°-（180°-2∠A），∠BIC=180°-
（180°-∠A），
∴[180°-（180°-2∠A）]+[180°-（180°-∠A）]=180°，
∴∠A=36°．
分析：根据中垂线定理及角平分线的性质分别将∠I和∠BOC用∠A表示出来，再根据∠I+∠BOC=180°可得出答案．
点评：本题考查三角形的内角和定理，难度不大，注意掌握中垂线及角平分线的性质．
∴∠BOC=180°-（180°-2∠A），∠BIC=180°-
（180°-∠A），∴[180°-（180°-2∠A）]+[180°-
（180°-∠A）]=180°，∴∠A=36°．
分析：根据中垂线定理及角平分线的性质分别将∠I和∠BOC用∠A表示出来，再根据∠I+∠BOC=180°可得出答案．
点评：本题考查三角形的内角和定理，难度不大，注意掌握中垂线及角平分线的性质．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
如图点O是△ABC的边AB、AC的中垂线的交点，I是∠ABC、∠ACB的平分线的交点，且∠I+∠BOC=180°，求∠BAC的度数．
如图点G是△ABC的重心，连接AG并延长交BC于D，则点D是BC的
如图点P是△ABC的边AC上一点，∠APB=∠ABC，AP=2，CP=6 则AB=
如图点I是△ABC的内心，∠BIC=130°，则∠BAC=（ ）