Question

【题目】如图，，，，．求和的长．

Answer 1

【答案】，．

【解析】

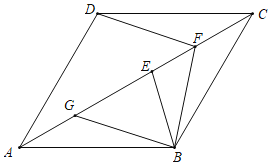
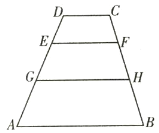
过C作CQ∥AD，交GH于N，交EF于M，交AB于Q，则可判断四边形AQCD为平行四边形，所以AQ=CD=6，同理可得EM=EM=CD=6，则BQ=AB-AQ=6，再利用平行线分线段成比例定理得到DE：EG：GA=CF：HF：HB=3：4：5，然后根据平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例得到MF：BQ=CF：CB=3：12，NH：BQ=CH：CB=7：12，则可计算出MF和NH，从而得到GH和EF的长

解：过作，交于点，交于点，交于，如图，

∵，

∴四边形为平行四边形．

∴，

同理可得．

∴．

∵，

∴．

∵，

∴，．

∴，．

∴，．

故答案为：，．