题目内容
(
a2b3c)•(
ab)= ;2m2•(-
mn)3= .
| 2 |
| 3 |
| 9 |
| 4 |
| 1 |
| 2 |
考点:单项式乘单项式
专题:
分析:根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可.
先算积的乘方,再根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可.
先算积的乘方,再根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可.
解答:解:(
a2b3c)•(
ab)=
a3b4c;
2m2•(-
mn)3
=2m2•(-
m3n3)
=-
m5n3.
故答案为:
a3b4c;-
m5n3.
| 2 |
| 3 |
| 9 |
| 4 |
| 3 |
| 2 |
2m2•(-
| 1 |
| 2 |
=2m2•(-
| 1 |
| 8 |
=-
| 1 |
| 4 |
故答案为:
| 3 |
| 2 |
| 1 |
| 4 |
点评:本题考查了积的乘方、单项式与单项式相乘,熟练掌握运算法则是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
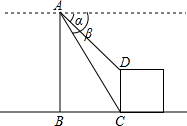 关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ;
关于三角函数有如下的公式:sin(α+β)=sinαcosβ+cosαsinβ;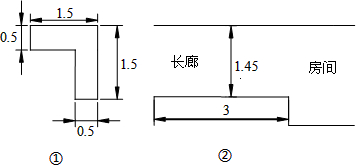
 如图,直线AB和CD相交于点O,∠DOE是直角,若∠1=30°,则∠2=
如图,直线AB和CD相交于点O,∠DOE是直角,若∠1=30°,则∠2=