题目内容
 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,求PD的长.
如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,求PD的长.考点:角平分线的性质,含30度角的直角三角形
专题:
分析:过点P作PE⊥OA于点E,根据角平分线上的点到角的两边的距离相等可得PE=PD,再根据两直线平行,内错角相等可得∠POD=∠OPC,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB,再根据直角三角形30°角所对的直角边等于斜边的一半得出PE=
PC=2,则PD=2.
| 1 |
| 2 |
解答: 解:过点P作PE⊥OA于点E,
解:过点P作PE⊥OA于点E,
∵OP是∠AOB的平分线,
∴PE=PD.
∵PC∥OB,
∴∠POD=∠OPC,
∴∠PCE=∠POC+∠OPC=∠POC+∠POD=∠AOB=30°,
∴PE=
PC=2,
∴PD=2.
 解:过点P作PE⊥OA于点E,
解:过点P作PE⊥OA于点E,∵OP是∠AOB的平分线,
∴PE=PD.
∵PC∥OB,
∴∠POD=∠OPC,
∴∠PCE=∠POC+∠OPC=∠POC+∠POD=∠AOB=30°,
∴PE=
| 1 |
| 2 |
∴PD=2.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,以及三角形的一个外角等于与它不相邻的两个内角的和,作辅助线构造含30°角的直角三角形是解题的关键.

练习册系列答案
相关题目
在函数y=(x+1)2+3中,y随x增大而减小,则x的取值范围为( )
| A、x>-1 | B、x>3 |
| C、x<-1 | D、x<3 |
一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是( )
| A、15或17 |
| B、16或15 |
| C、15 |
| D、16或15或17 |
在式子m+5、ab、a+b<1、x、-ah、s=ab中代数式的个数有( )
| A、6个 | B、5个 | C、4个 | D、3个 |
 如图,在△ABC中,AC⊥BC,CD⊥AB垂足为D.
如图,在△ABC中,AC⊥BC,CD⊥AB垂足为D.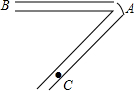 工人李师傅想制作一个如图所示的“V”形零件,他先把材料变成一个40°的锐角,然后准备在C处第二次加工拐弯,请你帮助他算一下,他应该怎样向外弯才能保证变过来的部分与AB保持平行?你的依据是什么?
工人李师傅想制作一个如图所示的“V”形零件,他先把材料变成一个40°的锐角,然后准备在C处第二次加工拐弯,请你帮助他算一下,他应该怎样向外弯才能保证变过来的部分与AB保持平行?你的依据是什么?