题目内容
20．若菱形ABCD的对角线AC、BD的长分别是6cm和8cm，则AB=5cm．分析 由菱形对角线的性质，相互垂直平分即可得出菱形的边长．
解答 解：解：根据题意，设对角线AC、BD相交于O，
则由菱形对角线性质知，AO=$\frac{1}{2}$AC=3cm，BO=$\frac{1}{2}$BD=4cm，且AO⊥BO，
在Rt△AOB中，∵AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5cm，
∴AB=5cm，
故答案为5cm．
点评 本题考查菱形性质的应用，解题的关键是记住菱形的对角线互相垂直平分，菱形的四条边相等．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
10．-1+2的值是（ ）
| A． | -1 | B． | 1 | C． | -3 | D． | 3 |
11．有两个标有数字的小球，小球上的数字分别为26，29，则这两个小球上的数字相乘的结果为（ ）
| A． | 217 | B． | 216 | C． | 215 | D． | 214 |
8．
如图，在矩形ABCD中，对角线AC，BD相交于点O，△ABO是等边三角形，AB=$\sqrt{3}$，则△AOD的面积为（ ）
如图，在矩形ABCD中，对角线AC，BD相交于点O，△ABO是等边三角形，AB=$\sqrt{3}$，则△AOD的面积为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{3}{2}$ | C． | $\frac{3\sqrt{3}}{4}$ | D． | $\frac{9}{4}$ |
15．下列二次根式中是最简二次根式的是（ ）
| A． | $\sqrt{14}$ | B． | $\sqrt{8}$ | C． | $\sqrt{\frac{2}{3}}$ | D． | $\sqrt{20}$ |
5．如图所示，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向不断移动，每移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0）…，那么A2017的坐标为（ ）
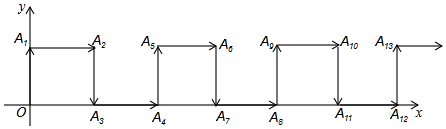
| A． | （2017，0） | B． | （1008，0） | C． | （1007，1） | D． | （1008，1） |
12．若a=（-$\frac{2}{3}$）-2，b=（-4）-1，c=（-$\frac{π}{2}$）0，则a、b、c的大小关系是（ ）
| A． | a＞b=c | B． | a＞c＞b | C． | c＞a＞b | D． | b＞c＞a |
9．下面各图中的∠1与∠2是对顶角的是（ ）
| A． |  | B． |  | C． |  | D． |  |
10．计算（14x3-21x2+7x）÷（-7x）的结果是（ ）
| A． | -x2+3x | B． | -2x2+3x-1 | C． | -2x2+3x+1 | D． | 2x2-3x+1 |