题目内容
8. 如图,在矩形ABCD中,对角线AC,BD相交于点O,△ABO是等边三角形,AB=$\sqrt{3}$,则△AOD的面积为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,△ABO是等边三角形,AB=$\sqrt{3}$,则△AOD的面积为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\frac{9}{4}$ |
分析 根据等高模型,可知S△AOD=S△AOD,求出△AOB的面积即可.
解答 解:∵△ABO是等边三角形,AB=$\sqrt{3}$,
∴S△AOB=$\frac{\sqrt{3}}{4}$•($\sqrt{3}$)2=$\frac{3\sqrt{3}}{4}$,
∵四边形ABCD是矩形,
∴OB=OD,
∴S△AOD=S△AOD=$\frac{3\sqrt{3}}{4}$.
故选C.
点评 本题考查等边三角形的性质、矩形的性质,等高模型等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
18.比-1小2017的数是( )
| A. | -2016 | B. | 2016 | C. | 2018 | D. | -2018 |
19.为了解2016年A市九年级学生学业水平考试的数学成绩,从中随机抽取了2000学生的数学成绩,下列说法正确的是( )
| A. | 2016年A市九年级学生是总体 | |
| B. | 样本容量是2000 | |
| C. | 2000名九年级学生是总体的一个样本 | |
| D. | 每一名九年级学生是个体 |
3.单项式-32xy2z3的次数和系数分别为( )
| A. | 6,-3 | B. | 6,-9 | C. | 5,9 | D. | 7,-9 |
17. 如图所示,以O为端点的射线共有( )
如图所示,以O为端点的射线共有( )
 如图所示,以O为端点的射线共有( )
如图所示,以O为端点的射线共有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
18.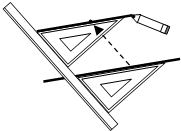 如图,过直线外一点作已知直线的平行线,其依据是( )
如图,过直线外一点作已知直线的平行线,其依据是( )
 如图,过直线外一点作已知直线的平行线,其依据是( )
如图,过直线外一点作已知直线的平行线,其依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 两直线平行,同位角相等 | D. | 两直线平行,内错角相等 |