题目内容
3.计算:(1)$\root{3}{64}$$-\sqrt{0}$-$\sqrt{2\frac{1}{4}}$
(2)($\sqrt{2}$)2-$\root{3}{27}$+$\sqrt{{9}^{2}}$
(3)$\sqrt{4}$-$\root{3}{8}$+$\root{3}{-\frac{1}{27}}$-(-$\frac{1}{3}$)2
(4)|1-$\sqrt{2}$|+|$\sqrt{2}$-3|
分析 (1)首先利用立方根和平方根的定义化简各数进而得出答案;
(2)首先利用立方根和平方根的定义化简各数进而得出答案;
(3)首先利用立方根和平方根的定义化简各数进而得出答案;
(4)直接利用绝对值的性质化简求出答案.
解答 解:(1)$\root{3}{64}$$-\sqrt{0}$-$\sqrt{2\frac{1}{4}}$
=4-0-$\sqrt{\frac{9}{4}}$
=4-$\frac{3}{2}$
=$\frac{5}{2}$;
(2)($\sqrt{2}$)2-$\root{3}{27}$+$\sqrt{{9}^{2}}$
=2-3+9
=8;
(3)$\sqrt{4}$-$\root{3}{8}$+$\root{3}{-\frac{1}{27}}$-(-$\frac{1}{3}$)2
=2-2-$\frac{1}{3}$-$\frac{1}{9}$
=-$\frac{4}{9}$;
(4)|1-$\sqrt{2}$|+|$\sqrt{2}$-3|
=$\sqrt{2}$-1+3-$\sqrt{2}$
=2.
点评 此题主要考查了实数运算,正确掌握立方根以及绝对值的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列不能铺满地面的正多边形组合是( )
| A. | 正五边形和正十边形 | B. | 正六边形和正三角形 | ||
| C. | 正方形和正八边形 | D. | 正方形和正三角形 |
8.下列各式由左边到右边的变形,属于因式分解的是( )
| A. | 6a2b=2•3•a•a•b | B. | x2-2x+1=x(x-2)+1 | ||
| C. | a2-b2=(a+b)(a-b) | D. | ax+ay+bx+by=a(x+y)+b(x+y) |
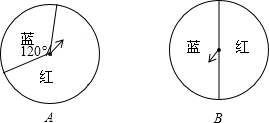 游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由. 看图填空:图中同位角4对,内错角2对,同旁内角3对.
看图填空:图中同位角4对,内错角2对,同旁内角3对.