题目内容
13.若△ABC∽△DEF,S△ABC:S△DEF=3:4,则△ABC与△DEF的相似比为$\sqrt{3}$:2.分析 由△ABC∽△DEF,S△ABC:S△DEF=3:4,根据相似三角形的面积比等于相似比的平方,即可求得答案.
解答 解:∵△ABC∽△DEF,S△ABC:S△DEF=3:4,
∴△ABC与△DEF的相似比为:$\sqrt{3}$:2.
故答案为:$\sqrt{3}$:2.
点评 此题考查了相似三角形的性质.注意相似三角形面积的比等于相似比的平方.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
1.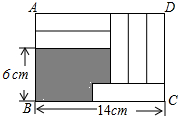 在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
 在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )| A. | 38cm2 | B. | 42cm2 | C. | 40cm2 | D. | 44cm2 |
8.-3的绝对值等于( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 小于3 |




 已知:∠1=∠2,CD=DE,EF∥AB.
已知:∠1=∠2,CD=DE,EF∥AB.


