题目内容
3．在实数范围内因式分解：2x2-3x-1=2（x-$\frac{3+\sqrt{17}}{4}$）（x-$\frac{3-\sqrt{17}}{4}$）．分析 令原式为0求出x的值，即可确定出因式分解的结果．
解答 解：令2x2-3x-1=0，
解得：x=$\frac{3±\sqrt{17}}{4}$，
则原式=2（x-$\frac{3+\sqrt{17}}{4}$）（x-$\frac{3-\sqrt{17}}{4}$）．
故答案为：2（x-$\frac{3+\sqrt{17}}{4}$）（x-$\frac{3-\sqrt{17}}{4}$）．
点评 此题考查了实数范围内分解因式，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
11．“把弯曲的公路改直，就能缩短路程”其中蕴含的数学道理是（ ）
| A． | 两点确定一条直线 | B． | 两点之间直线最短 | ||
| C． | 两点之间线段最短 | D． | 直线比曲线短 |
18．将一元二次方程x2-4x+3=0化成（x+m）2=n的形式，则n等于（ ）
| A． | -3 | B． | 1 | C． | 4 | D． | 7 |
已知，如图，点D．E分别在AB、AC上，点F在BC的延长线上，∠A=35°，∠ACF=105°，∠ADE=70°．求证：DE∥BF．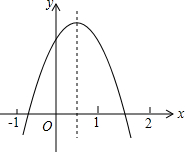
二次函数y=ax2+bx+c的图象如图所示，则下列式子