题目内容
19.若二项式4m2+1加上一个单项式后是一含m的完全平方式,则单式为±4m或4m4或$\frac{1}{16{m}^{2}}$.分析 式子4m2和1分别是2m和1的平方,可当作首尾两项,可作末尾两项,也可以作前两项.所以根据完全平方公式进行解答即可.
解答 解:当4m2和1分别当作首尾两项时,添加±4m可以构成完全平方式,即4m2±4m+1=(2m±1)2;
当4m2和1分别当作末尾两项时,添加4m4可以构成完全平方式,即4m4+4m2+1=(2m2+1)2;
当4m2和1分别当作前两项时,添加$\frac{1}{16{m}^{2}}$可以构成完全平方式,即4m4+1+$\frac{1}{16{m}^{2}}$=(2m+$\frac{1}{4m}$)2;
可以添加±4m或4m4或$\frac{1}{16{m}^{2}}$.
故答案是:±4m或4m4或$\frac{1}{16{m}^{2}}$.
点评 本题考查对完全平方公式灵活应用的能力,把握其公式结构特点是完成此类题的关键.

练习册系列答案
相关题目
11.下列由左到右的变形中,属于因式分解的是( )
| A. | x2+3x-4=x(x+3)-4 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | x2-4=(x+2)(x-2) | D. | (x-2)(x+2)=x2-4 |
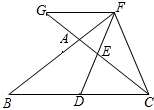 如图,在△ABC中,AB=AC,点D在BC上,点F在BA的延长线上,FD=FC,点E是AC与DF的交点,且ED=EF,FG∥BC交CA的延长线于点G.
如图,在△ABC中,AB=AC,点D在BC上,点F在BA的延长线上,FD=FC,点E是AC与DF的交点,且ED=EF,FG∥BC交CA的延长线于点G.