��Ŀ����
����Ŀ���Ķ����ϣ����һԪһ�η��̣���Ҫ���ݵ�ʽ�Ļ������ʣ��ѷ���ת��Ϊx��a����ʽ������Ԫһ�η����飬��Ҫͨ����Ԫ����ת��ΪһԪһ�η������⣻�����Ԫһ�η����飬��Ҫ����ת��Ϊ��Ԫһ�η��������⣻���һԪ���η��̣���Ҫ����ת��Ϊ����һԪһ�η������⣻����ʽ���̣���Ҫͨ��ȥ��ĸ����ת��Ϊ��ʽ�������⣬����̵Ľⷨ������ͬ���������Ƕ��õ�һ�ֹ�ͬ�Ļ�����ѧ˼�멁ת��������δ֪ת��Ϊ��֪����⣮
�á�ת��������ѧ˼�룬���ǻ����Խ�һЩ�µķ��̣�
���磬��һԪ���η���x3+x2��2x��0��ͨ����ʽ�ֽ����ת��Ϊx��x2+x��2����0��ͨ���ⷽ��x��0��x2+x��2��0���ɵ�ԭ����x3+x2��2x��0�Ľ⣮
�����磬������º�����֪���ķ��̣�![]() ��x��ͨ������ͬʱƽ������ת��Ϊ2x+3��x2����ã�x1��3��x2����1����Ϊ2x+3��0����x��0������x����1����ԭ���̵ĸ���x��3��ԭ���̵Ľ⣮
��x��ͨ������ͬʱƽ������ת��Ϊ2x+3��x2����ã�x1��3��x2����1����Ϊ2x+3��0����x��0������x����1����ԭ���̵ĸ���x��3��ԭ���̵Ľ⣮
��1�����⣺����x3+x2��2x��0�Ľ���x1��0��x2���� ����x3���� ����
��2����չ����![]() ��x��1�Ľ⣻
��x��1�Ľ⣻
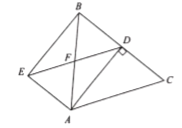
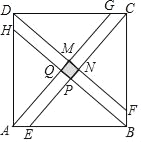
��3��Ӧ�ã���һ���߳�Ϊ1���������й���һ����ͼ��ʾ�������Σ���������ABCD�������ν�ȡAE��BF��CG��DH��![]() ������AG��BH��CE��DF���õ�������MNPQ����С������MNPQ��ͼ����Ӱ���֣��ı߳�Ϊ
������AG��BH��CE��DF���õ�������MNPQ����С������MNPQ��ͼ����Ӱ���֣��ı߳�Ϊ![]() ����n��ֵ��
����n��ֵ��
���𰸡���1��1����2����2�������������3��n��ֵΪ9��
��������
��1��������ʽ�ֽⷨ�����ɵó����ۣ�
��2���ȷ�������ƽ��ת������ʽ���̣�����һԪ���η��̵Ľ⣬��������飻
��3���ȸ��ݹ��ɶ������AG�������ó�sin��AGD�� ���ٹ����ֱ�������Σ��ó�sin��EAW��
���ٹ����ֱ�������Σ��ó�sin��EAW��![]() �������������̣����ã�2���ķ�����˷��̼��ɵó����ۣ�
�������������̣����ã�2���ķ�����˷��̼��ɵó����ۣ�
��1����x3+x2��2x��0��
��x��x��1����x+2����0
��x��0��x��1��0��x+2��0��
��x1��0��x2��1��x3����2��
�ʴ�Ϊ1����2��
��2��������
![]() ��x��1������ƽ���ã�3x2��3x��2����x��1��2��
��x��1������ƽ���ã�3x2��3x��2����x��1��2��
��x��![]() ��x����1��
��x����1��
��3x2��3x��2��0��x��1��0��
��x����1����ԭ���̵Ľ⣬x��![]() ��ԭ���̵Ľ⣻
��ԭ���̵Ľ⣻
��3����ͼ��
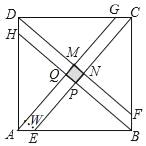
���ı���ABCD�������Σ�
���ADC��90����
CD��AB��
���AGD����GAB��
��CG��AE��CG��AE��
���ı���AECG��ƽ���ı��Σ�
��AG��EC����E��EW��PQ��AQ��W��
���ı���PQWE��ƽ���ı��Σ�
��EW��PQ��![]() ��
��
���ı���MNPQ�������Σ�
���PQA��90����
���AWE��90����
��Rt��ADG��AD��1��DG��1��![]() ��
��
���ݹ��ɶ����ã�AG��![]()
![]() ��
��
��sin��AGD��![]() ��
�� ��
��
��Rt��AWD��AE��![]() ��EW��
��EW��![]() ��
��
��sin��EAW��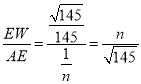 ��
��
�ߡ�AGD����EAW��
�� ��
��![]() ��
��
����ƽ���ã�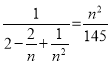 ��
��
��2n2��2n+1��145��
��n2��n��72��0��
����n��9����n+8����0��
��n��9��n����8������n��0�������ȥ����
��n��9��
����n��ֵΪ9��

����Ŀ��ijˮ�����������·�����һ�������е�ˮ����ƽ���ۼ�Ϊ10Ԫ/ǧ�ˣ���������Ϊ1000ǧ��.���г����飬��������ˮ���۸������xԪ/ǧ�ˣ����·�������y��ǧ�ˣ���x��Ԫ/ǧ�ˣ�֮�����һ�κ�����ϵ�����ҵõ��˱��е����ݣ�
�۸�x��Ԫ/ǧ�ˣ� | 7 | 5 |
�۸�y��ǧ�ˣ� | 2000 | 4000 |
��1����y��x֮��ĺ�������ʽ��
��2����֪����ˮ�����·ݵijɱ���Ϊ5Ԫ/ǧ�ˣ����·ݵijɱ���Ϊ4Ԫ/ǧ�ˣ�Ҫʹ���·����۸���ˮ��������������·�����20����ͬʱ��Ҫ�ù˿͵õ�ʵ�ݣ���ô����ˮ���۸�ÿǧ��Ӧ����������Ԫ?