题目内容
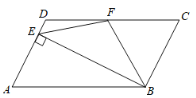
【题目】如图，在
中，
，
，
为
边上的高，过点
作
，过点
作
，
与
交于点
，
与交于点
，连结
．
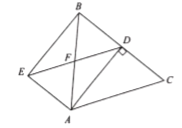
（1）求证：四边形
是矩形；
（2）求四边形的周长．
【答案】（1）见详解；（2）
【解析】
（1）利用平行四边形的性质和矩形的判定定理推知平行四边形AEBD是矩形．
（2）在Rt△ADC中，由勾股定理可以求得AD的长度，由等腰三角形的性质求得BD的长度，即可得出结果．
（1）证明：∵AE∥BC，DE∥AC，
∴四边形AEDC是平行四边形．
∴AE＝CD．
在△ABC中，AB＝AC，AD为BC边上的高，
∴∠ADB＝90°，BD＝CD．
∴BD＝AE．
∴四边形AEBD是矩形．
（2）解：在Rt△ADC中，∠ADB＝90°，AC＝9，BD＝CD＝
BC＝3，
∴AD＝
．
∴四边形AEBD的周长＝．
阅读快车系列答案【题目】小东根据学习函数的经验，对函数
的图象与性质进行了探究．下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数的自变量x的取值范围是 ；
（2）下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________；
（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点. 根据描出的点，画出函数的大致图象；
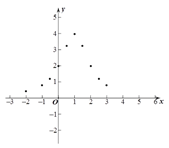
（4）结合函数图象，请写出函数的一条性质：______________________.
（5）解决问题：如果函数与直线y=a的交点有2个，那么a的取值范围是______________ .
【题目】某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：
①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
时间（第x天） | 1 | 3 | 6 | 10 | … |
日销售量（m件） | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天） | 1≤x＜50 | 50≤x≤90 |
销售价格（元/件） | x+60 | 100 |
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
