题目内容
正方形ABCD的对角线AC、BD相交于O,直角三角板EFG的直角顶点E在线段AC上,EF、EG与BC、CD边相交于M、N.
(1)如图1,若E点与O点重合,求证:EM=EN;
(2)如图2,若E点不与O点重合:
①EM还等于EN吗?说明理由;
②试找出MC、CN、EC三者之间的等量关系,并说明理由.
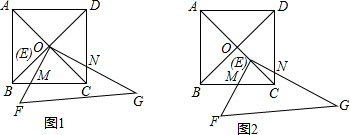
(1)如图1,若E点与O点重合,求证:EM=EN;
(2)如图2,若E点不与O点重合:
①EM还等于EN吗?说明理由;
②试找出MC、CN、EC三者之间的等量关系,并说明理由.

考点:正方形的性质,全等三角形的判定与性质
专题:常规题型
分析:(1)要证明EM=EN,证明△OBM≌△OCN即可解本题;
(2)同理可证△OBM≌△OCN;
(3)找出MC+NC与CG的关系,找到CG与EC的关系即可解本题.
(2)同理可证△OBM≌△OCN;
(3)找出MC+NC与CG的关系,找到CG与EC的关系即可解本题.
解答:解:(1)在正方形ABCD中,OA=OB=OC=OD,且∠OBC=∠OCD,∠BOC=90°,
∵∠FOG=90°,
∴∠BOM=∠BOC-∠MOC=90°-∠MOC,∠CON=∠FOG-∠MOC=90°-∠MOC,
∴∠BOM=∠CON,
在△OBM和△OCN中,
,
∴△OBM≌△OCN(ASA),
∴EM=EN;
(2)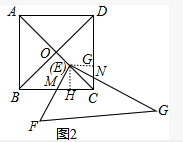
过E作EH⊥BC,EG⊥CD,
由正方形ABCD可知,AC平分∠BCD,
∴EH=EG,
∵∠HEG=360°-∠EHC-∠EGC-∠HCG=90°,
∴∠MEH=∠NEG,而∠EHM=∠EGN=90°,
∴△EMH≌△ENG,
∴EM=EN;
(3)由△EMH≌△ENG可知,MH=NG,而EG=HC,
∴MC+NC=MH+HC+NC=NG+EG+NC=EG+CG=2CG,
∵CG=
EC,
∴MC+NC=
EC.
答:(1)EM=EN,(2)EM=EN,(3)MC+NC=
EC.
∵∠FOG=90°,
∴∠BOM=∠BOC-∠MOC=90°-∠MOC,∠CON=∠FOG-∠MOC=90°-∠MOC,
∴∠BOM=∠CON,
在△OBM和△OCN中,
|
∴△OBM≌△OCN(ASA),
∴EM=EN;
(2)

过E作EH⊥BC,EG⊥CD,
由正方形ABCD可知,AC平分∠BCD,
∴EH=EG,
∵∠HEG=360°-∠EHC-∠EGC-∠HCG=90°,
∴∠MEH=∠NEG,而∠EHM=∠EGN=90°,
∴△EMH≌△ENG,
∴EM=EN;
(3)由△EMH≌△ENG可知,MH=NG,而EG=HC,
∴MC+NC=MH+HC+NC=NG+EG+NC=EG+CG=2CG,
∵CG=
| ||
| 2 |
∴MC+NC=
| 2 |
答:(1)EM=EN,(2)EM=EN,(3)MC+NC=
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
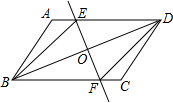 已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.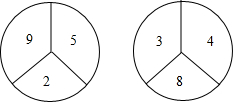 有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
 如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=
如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=