题目内容
如图,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合),现将 PAB沿PB翻折,得到
PAB沿PB翻折,得到 PDB;再在OC边上选取适当的点E,将
PDB;再在OC边上选取适当的点E,将 POE沿PE翻折,得到
POE沿PE翻折,得到 PFE,并使直线PD、PF重合。
PFE,并使直线PD、PF重合。
(1)设P(x,0),E(0,y),求y关于x的函数关系式及自变量x的取值范围,并求出y的最大值;
(2)如图 ,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;
,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;
|
|
 PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标。
PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标。
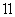 ②
②
解


① ②
(1)△PAB≌△PDB, △POE≌△PFE
∴∠APB=∠DPB ∠OPE=∠FPE
∵∠APB+∠DPB+∠OPE+∠FPE=1800
∴∠APB+∠OPE=900
∵∠OPE+∠OEP=900
∴∠APB=∠0EP
∵∠EOP=∠PAB=900
∴△POE∽△BAP
∴
∵A(4,0),C(0,3),E(0,y),P(x,0)
∴ 即
即

∵
而 ∴x=2时,
∴x=2时,
(2)四边形DPAB、EOPF都为正方形
∴AP=AB=3,OE=OP=4-3=1
∴E(0,1) P(1,0)
∵B(4,3)
∴过点P、B、E的抛物线的函数关系式为:

存在,Q(4,3)或(5,6)
由(2)知∠EPB=900
即点Q与点B重合时满足条件
直线PB为y=x-1,与y轴交于点(0,-1)
∴将直线PB向上平移2个单位则过点E(0,1)
∴该直线为y=x+1
由 解之得
解之得
∴Q(5,6)
∴该抛物线上存在两点Q(4,3)或(5,6)满足条件

某商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
| 类别 | 冰箱 | 彩电 |
| 进价(元/台) | 2 320 | 1 900 |
| 售价(元/台) | 2 420 | 1 980 |
(1) 按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的政府补贴?
(2)为满足农民需求,商场决定用不超过85 000元采购冰箱、彩电共40台, 且冰箱的数量不少于彩电数量的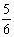 。
。
①请你帮助该商场设计相应的进货方案;
②哪种进货方案商场获得利润最大(利润=售价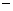 进价),最大利润是多少?
进价),最大利润是多少?


 在
在 轴上,且
轴上,且 , 分别过点
, 分别过点 轴的平行线,与反比例函数
轴的平行线,与反比例函数 的图像分别交于点
的图像分别交于点 ,分别过点
,分别过点 , 连接
, 连接 得到n个阴影三角形 那么图中第n个阴影三角形的面积是_______ 。
得到n个阴影三角形 那么图中第n个阴影三角形的面积是_______ 。 
 中自变量
中自变量 的取值范围是 ;
的取值范围是 ;
 A.
A. B.
B. C.
C. D.
D.
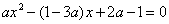
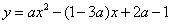 的对称轴是直线x=-2;
的对称轴是直线x=-2;