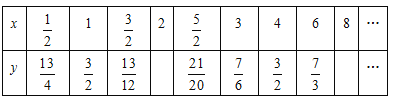
题目内容
【题目】定义：在平面直角坐标系中，我们将函数
的图象绕原点
逆时针旋转
后得到的新曲线
称为“逆旋抛物线”.
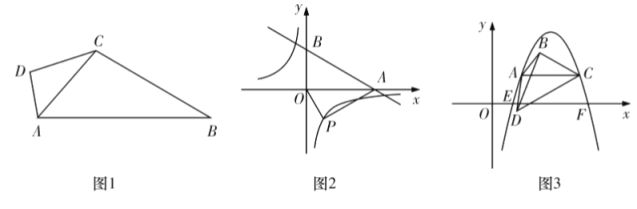
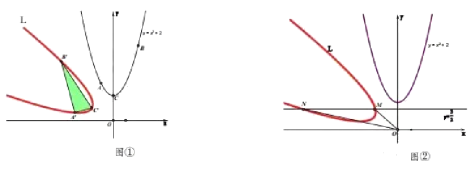
（1）如图①，己知点
，
在函数的图象上，抛物线的顶点为
，若上三点
、
、
是
、
、旋转后的对应点，连结
，
、
，则
__________；
（2）如图②，逆旋抛物线与直线
相交于点
、
，则
__________．
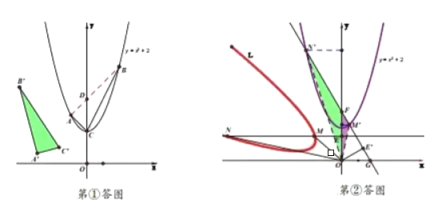
【答案】3； 
【解析】
（1）求出点A、B的坐标，再根据割补法求△ABC的面积即可得到
；
（2）将旋转后的MN和抛物线旋转到之前的状态，求出直线解析式及交点坐标，利用割补法求面积即可．
解：（1）在
上，令x=0，解得y=2，
所以C（0，2），OC=2，
将
，
代入，
解得a=3，b=2，
∴
，
，
设，的直线解析式为
，
则
，
解得
，
直线AB解析式为
，令x=0，
解得，y=4，即OD=4，
∴
，
∴
（2）如图，由旋转知，
，
，
∴
，
，
直线
，令
，得
∴
∴
∴
练习册系列答案
相关题目
