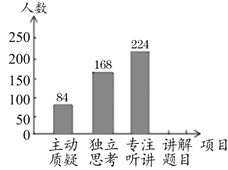
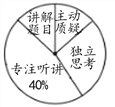
题目内容
【题目】如图,在由边长为![]() 个单位长度的小正方形组成的
个单位长度的小正方形组成的![]() 网格中,已知点
网格中,已知点![]() ,
,![]() ,
,![]() ,
,![]() 均为网格线的交点.
均为网格线的交点.
(1)在网格中将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后的图形
,画出旋转后的图形![]() ;
;
(2)在网格中将![]() 放大
放大![]() 倍得到
倍得到![]() ,使
,使![]() 与
与![]() 为对应点.
为对应点.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据旋转的性质,依据对应点与旋转中心的连线相等且夹角为90°找出旋转后各个对应点的位置,顺次连接即可;
(2)根据勾股定理分别求出AB,BC,AC的长,根据题意可知两个三角形的相似比为1:2,进而求出DE,EF,DF的长度,在网格中找出点E,F,再顺次连接D,E,F即可得出结果.
解:(1)如图所示,![]() 即为所求
即为所求
(2)根据勾股定理可得,AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() ,
,
∵△ABC与△DEF的相似比为1:2,
∴DE=2![]() ,EF=2
,EF=2![]() ,DF=2
,DF=2![]() ,
,
点E,F的位置如图所示,顺次连接点D,E,F,则![]() 即为所求.
即为所求.


练习册系列答案
相关题目