题目内容
20. 如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
分析 (1)连结OE,如图,由BE平分∠ABD得到∠OBE=∠DBO,加上∠OBE=∠OEB,则∠OBE=∠DBO,于是可判断OE∥BD,再利用等腰三角形的性质得到BD⊥AC,所以OE⊥AC,于是根据切线的判定定理可得AC与⊙O相切;
(2)设⊙O半径为r,则AO=10-r,证明△AOE∽△ABD,利用相似比得到$\frac{10-r}{10}$=$\frac{r}{6}$,然后解方程求出r即可.
解答 解:(1)AC与⊙O相切.理由如下:
连结OE,如图,
∵BE平分∠ABD,
∴∠OBE=∠DBO,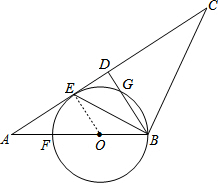
∵OE=OB,
∴∠OBE=∠OEB,
∴∠OBE=∠DBO,
∴OE∥BD,
∵AB=BC,D是AC中点,
∴BD⊥AC,
∴OE⊥AC,
∴AC与⊙O相切;
(2)设⊙O半径为r,则AO=10-r,
由(1)知,OE∥BD,
∴△AOE∽△ABD,
∴$\frac{AO}{AB}$=$\frac{OE}{BD}$,即$\frac{10-r}{10}$=$\frac{r}{6}$,
∴r=$\frac{15}{4}$,
即⊙O半径是$\frac{15}{4}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.解决(2)小题的关键是利用相似比构建方程.

练习册系列答案
相关题目
12.用棋子摆出如图所示的一组“口”字,按照这种方法照,则摆第n(n为正整数)个“口”字需用棋子( )枚.


| A. | 4n | B. | 4n-4 | C. | 4n+4 | D. | n2 |
 如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,若AE=13,求AF的长度.
如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,若AE=13,求AF的长度. 已知△ABC中,AB=AC=8cm,∠A=50°,AB的垂直平分线MN分别交AB于D,交AC于E,BC=6cm.求:
已知△ABC中,AB=AC=8cm,∠A=50°,AB的垂直平分线MN分别交AB于D,交AC于E,BC=6cm.求: